素数とは?中学数学で押さえておきたいポイント

素数って何?基本を知ろう
素数の定義をわかりやすく
素数とは、「1とその数自身の積でしか表せない自然数のこと」です。
言い換えると、「1とその数以外に約数ををもたない(約数が2つの)自然数」が素数となります。
2、3、5、7、・・・
などが素数ですが、例えば7は、1と7でしかわり切れませんから、素数です。
4や6は、1とその数自身でもわり切れますし、それぞれ2と3でもわり切れますので、素数ではありません。
素数を中学数学で学ぶ理由
素数は、数学の基礎となり、中学数学・高校数学を学ぶうえで必要不可欠な知識となります。
中学では、素数は「素因数分解」や「平方根」で使います。
自然数を素数の積だけで表す素因数分解では、言うまでもなく素数が重要な役割をもっています。
また、小学校5年生で習う「最大公約数・最小公倍数」でも、実は素数が鍵となっています。
数学の基礎となる素数はしっかりと理解を深めておく必要があります。
素数は中学数学でどのように使うの?
素因数分解で使う例
自然数を素数の積だけで表すことを素因数分解といいます。
素因数分解の基本手順はしたのようになります。
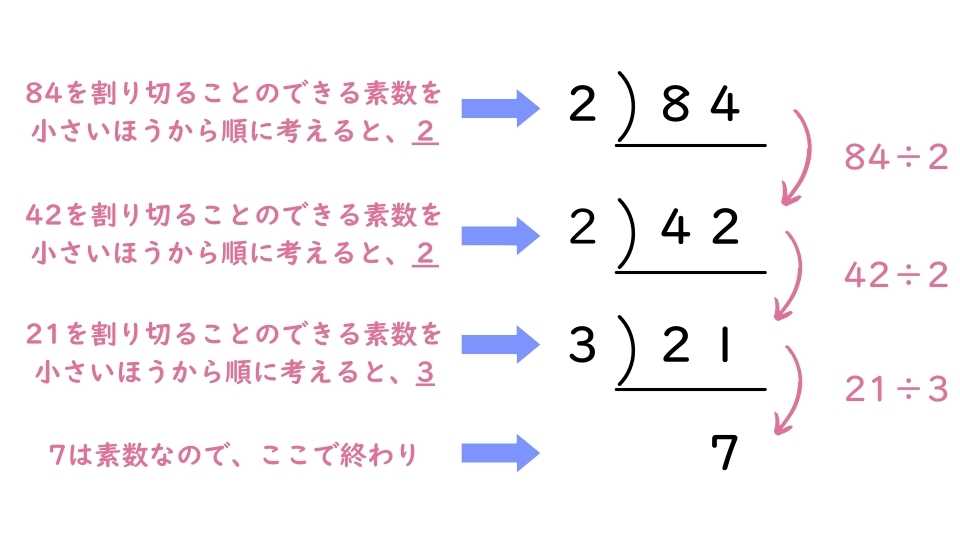
したがって、84を素因数分解すると、2×2×3×7となります。(実際の問題に答える際には、2²×3×7としましょう。)
最大公約数・最小公倍数の計算での役割
先ほど、最大公約数・最小公倍数で素因数分解が使えると書きましたが、どのように使うのでしょうか。
たとえば、90と162の最大公約数と最小公倍数を考えます。
90と162をそれぞれ素因数分解すると、こうなります。
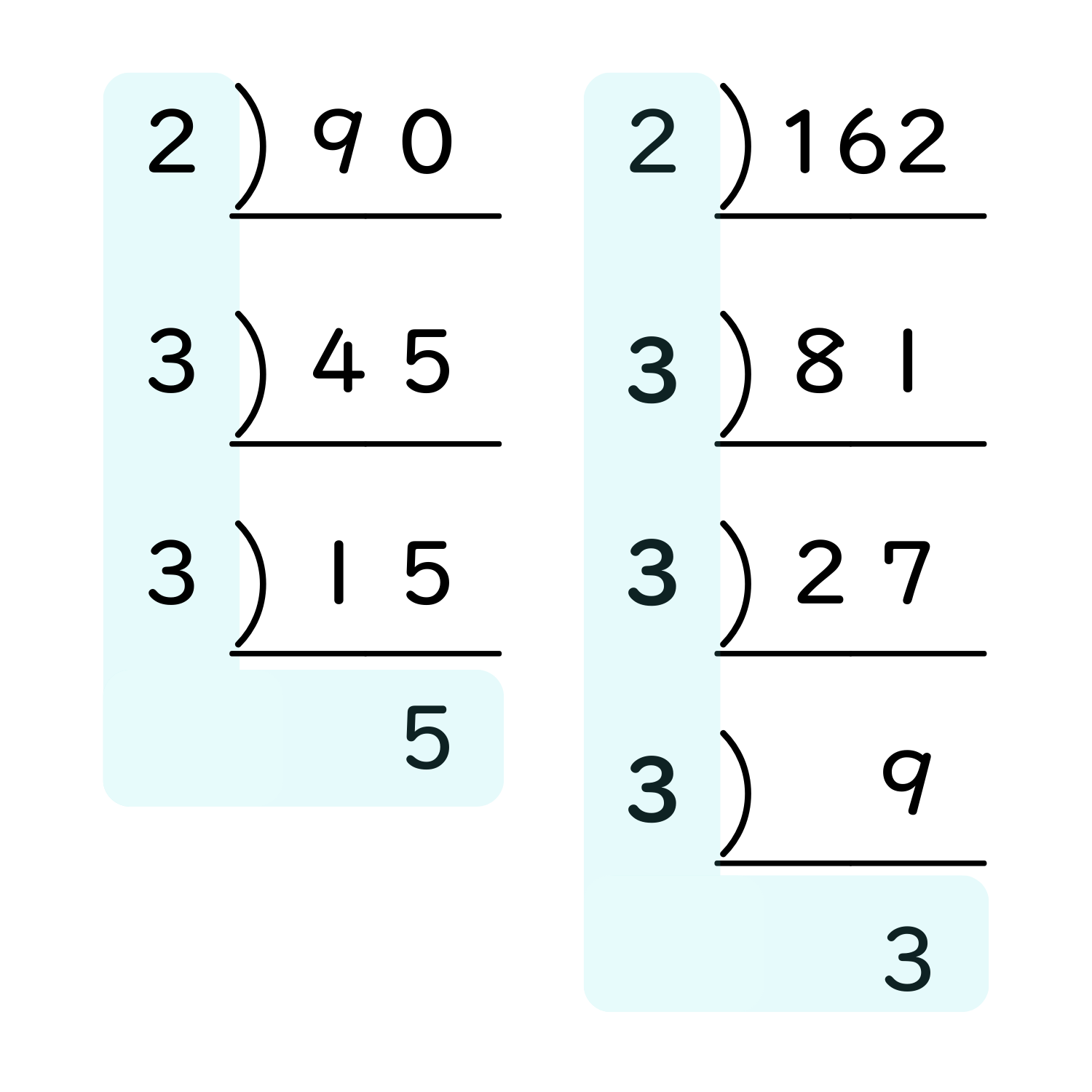
これを、下のように縦にそろえて書きます。
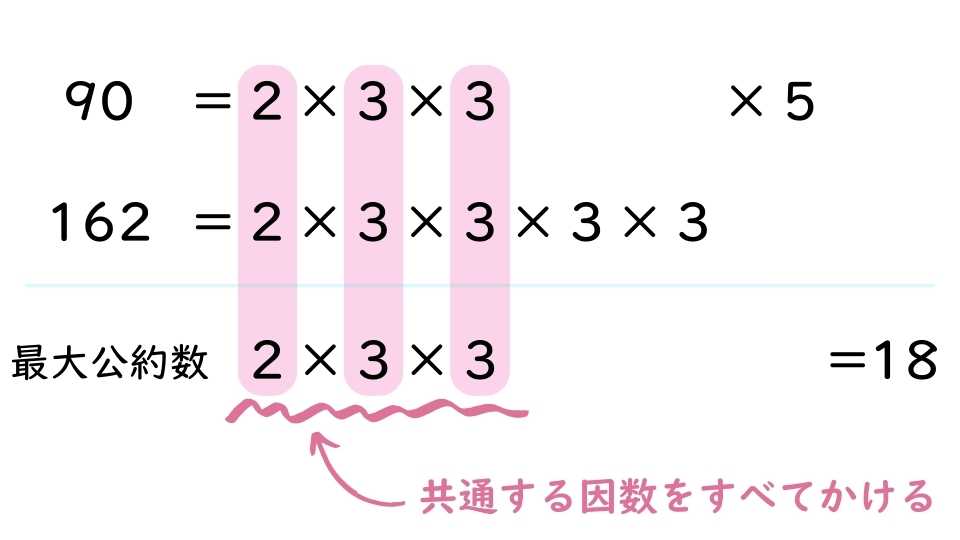
90と162の最大公約数は、したのように考えて、18だということがわかります。
90と162の最小公倍数は、したのように考えて、810だということがわかります。
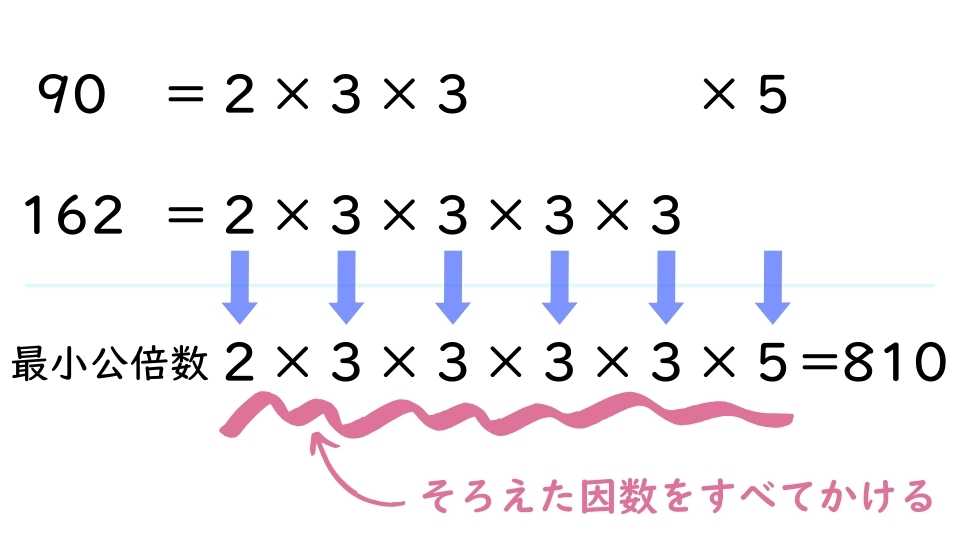
このように、最大公約数や最小公倍数を求める際には、素因数分解が役立ちます。
素数を見分ける方法
小さな数でわり算してみる
素数かどうかを見分けるために、小さな数でわり算をしてみるという方法があります。
【手順】
- 1. まず2でわってみる
偶数はすべて2でわり切れるので、2以外の偶数は素数ではありません。
例:4、6、8…は2でわり切れるので素数ではない。 - 2. 次に3でわる
3でわり切れる場合、その数も素数ではありません。
例:9、12、15…は3でわり切れるので素数ではない。 - 3. 5でわる
最後の数字が0か5で終わる数は、5でわり切れるため、素数ではありません。
例:10、15、20…は5でわり切れるので素数ではない。 - 4. 7、11、13、19…と暗記している素数でわる
エラトステネスの篩(ふるい)を使う方法
こちらの方法は、中学数学では習わないのですが、
「エラトステネスのふるい」という名の通り、ふるいにかけるように、多くの数のなかから素数を見つけのに便利です。
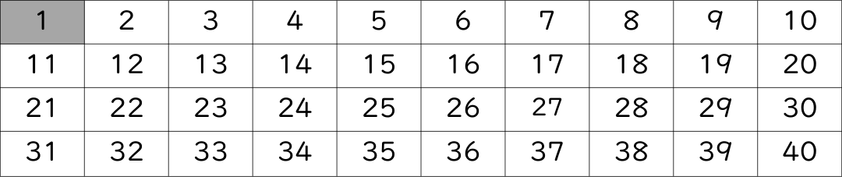
この方法を使って、1~40までの範囲の素数を見つけてみましょう。
【手順】
- 1. 1を消す
- 2. 最も小さい素数を残したまま、その素数の倍数をすべて消す。
この場合は、2を残して、2以外の2の倍数をすべてふるい落とします。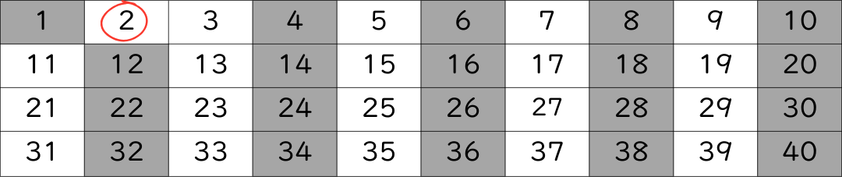
- 3. 残っている中で最も小さい素数を残したまま、その素数の倍数をすべて消す
この場合は、3を残して、3以外の3の倍数をすべてふるい落とします。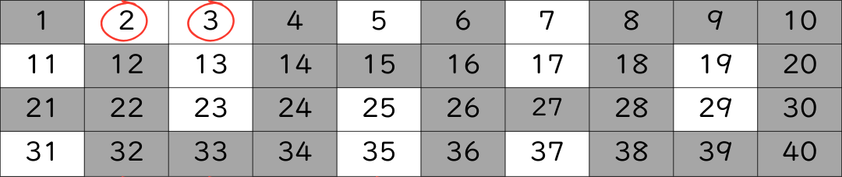
- 4. 手順3を最後まで繰り返す。
4はすべてふるい落とされているので、5を残して、5以外の5の倍数をすべてふるい落とします。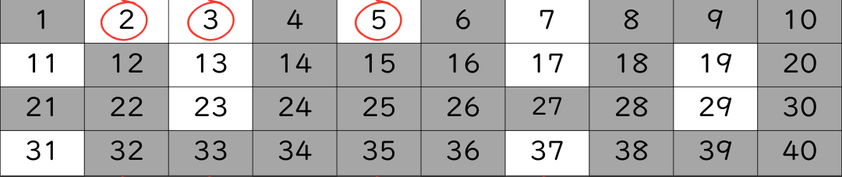
最後まで繰り返すと、下図のようになります。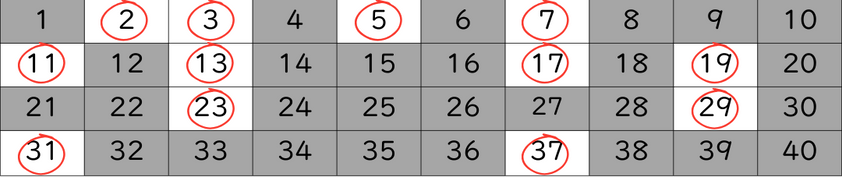
中学のテストでよく出る素数判定問題
中学のテストでは、ある数が素数かどうかを見分ける問いがよく出題されます。
例えば、
問題:101は素数か答えなさい
解答:101の約数は「1」と「101」の2つなので、101は素数である。
などです。
上記で紹介した方法などを用いて、素数かどうかを見分けます。
中学では覚えておくべき素数
中学の問題では、少なくとも【2,3,5,7,11,13,17,19】あたりまでの素数を暗記しておくとよいでしょう。
暗記をしておくことで、素数を見分ける問題が楽に解けるようになります。
もちろん、素数はずっと続いていきますので、興味があれば暗記してみても面白いかもしれないですね。
素数に関するよくある質問
・1は素数じゃないの?
素数の定義をみてみると、「1とその数以外に約数ををもたない(約数が2つの)自然数」となっています。
たとえば、2の約数は1と2の2つ、7の約数は1と7の2つ。
1は、約数が1自身の1つだけしかないので、素数ではないということになります。
・なぜ2は素数なのか?
なんとなく、2は偶数だから素数ではない気がしてしまいますが、2は素数です。
2は、「1」と「2」自身の2つの約数をもつ自然数なので、2は素数となります。
うっかりミスで、2が素数ではないと勘違いしないようにしましょう。
・素数は無限にあるの?
素数は無限に存在します。
素数が無数に存在することの証明は、色々な方法でされています。
有名なのは、背理法によるユークリッドの証明です。こちらは紀元前に発見されたものです。
そのほかにも、フェルマー数を用いたゴールドバッハの証明や、2006年に発表されたサイダックの証明などがあります。
・素数は何年生で学ぶ?
素数は、中学1年生で学びます。
現行の学習指導要領では、素数を1年において扱うことにより、
素因数分解を自然数、素数、倍数、約数、公倍数、公約数などと関連づけ、
整数の性質を探るひとつの道具として利用することができるとしています。
参考:文部科学省「中学校学習指導要領(平成29年告示)解説」2017年
▼文部科学省ホームページ
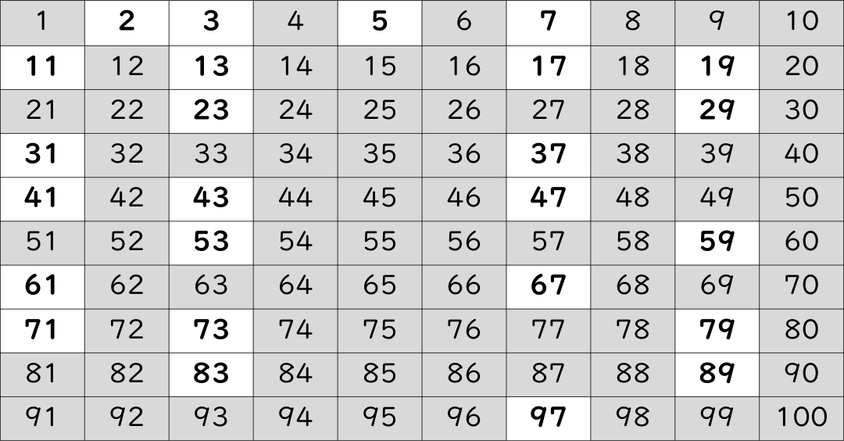
・100までの素数リストは?
1~100までに、素数は
「 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97」があり、全部で25個あります。
下図の白い背景のマスが、素数です。
素数の面白い応用例
素数は、とても不思議な数字です。
身近でも、素数の面白い応用例や、素数に絡んだ不思議なことがたくさんあります。
インターネットの暗号に使われる素数
インターネット上の情報を守るのに「暗号化」という技術が使われていますが、この暗号化において素数が重要な役割を担っています。
とある文書があったとき、素数×素数のかけ算で文書に暗号をかけます。
第三者には、かけ算の結果が公開されています。
暗号を元の文書に戻すためには別の鍵が必要です。
この鍵を得るためには、自然数=素数×素数と、逆の計算をしなければいけません。
地道に計算するので、素数の桁が大きいほど大変です。
簡単な例で考えると、19×23のかけ算はひっ算を使えばすぐできるけど、437=19×23を逆の計算をするのは大変ですよね。
この作業は、コンピューターでも膨大な時間がかかるため、インターネットのセキュリティでは素数が重要な役割を担っているということです。
自然界の不思議:セミと素数の関係
素数ゼミとよばれるセミを聞いたことがあるでしょうか。
素数ゼミとは、生き残り戦略のために、13年、もしくは17年の間、地中にいるセミのことです。
それでは、なぜ素数である13年、もしくは17年の間、地中にいることが生き残り戦略となるのでしょうか。
その秘密は、最小公倍数にあります。
例えば、13年ゼミ周期で土の中から出てくる素数ゼミに、3年周期で発生する天敵がいたとします。

天敵が3年周期で発生していても、同じ年に13年周期ゼミが地上に出るのは、上の表のように39年経ったときのみです。
39は、13と3の最小公倍数です。13が素数であるため、3を約数に持たないことから、この最小公倍数が大きくなっています。
仮にセミの地上にいる期間が1年短い12年だとすると、地上に出れば毎回3年周期で発生している天敵がいるということになってしまいます。
セミの発生周期が素数であることは、その数自身しか約数がない自然数である素数を地上にでる周期にすることで、
天敵とできるだけ出会わないようにする、セミの生き残り戦略と考えることができます。
「わからないをわかるにかえる数学」

ここでPR!
今回解説した「素数」は中学1年生で学びます。
そんな中学生向けの中学生向けの超基礎シリーズが、こちらの『わからないをわかるにかえる』。
平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。
「わからないをわかるにかえる高校入試数学」

人気の超基礎シリーズ「わからないをわかるにかえる」の高校入試対策版です。
中学3年間の内容を基礎からおさらいできます。
やさしい言葉遣いやイラストで、とっつきやすいのが特徴で、苦手な分野が多く、易しめから入りたい人はチェックしてみてください。
「大人の教科書ワーク 数学」

日常の悩みや疑問を、小中学校の教科書で解決!
それがこちらの『大人の教科書ワーク』です。
実は、今回の記事のなかで紹介した「インターネットの暗号に使われる素数」や「セミと素数の関係」について、
この『大人の教科書ワーク数学』ではさらに詳しく書かれています!
この本では、このような数学にまつわる面白いトピックをたくさんとりあげています。
「大人の学び直し」がテーマの本ですが、小中学校の教科書で習う算数・数学の内容を用いながら、
日常のあらゆる疑問に答える形式になっているので、いままさに数学を学んでいる中学生が数学を学ぶ楽しさを知るのにもぴったりです!
まとめ
いかかでしたか。
今回の記事では、素数の定義から中学数学で押さえておきたいポイント、素数を応用した例までご紹介しました。
素数は数学の基礎であると同時に、どこか不思議な数字ですよね。
素数を通じて数学の魅力に触れ、ぜひ今の学びを深めてみてください!

関連記事
算数・数学の不思議
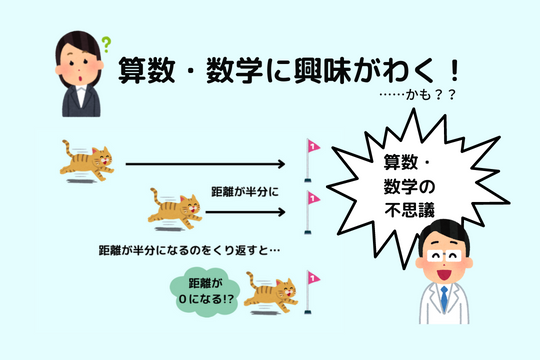
こんにちは! 突然ですが……みなさん、算数・数学は好きですか? 「池のまわりを反対方向に回りがち」「妹の忘れ物に気づいた兄が同じ道を追いかけがち」など、 算数・数学の問題には楽しいツッコミどころがたくさんありますが、 「わかっていて解いたのに計算ミスで減点」「図形の問題に苦手意識があっていつも手が出ない」など、 好きではない方も多い教科ではないでしょうか。 かく言う私も、今でこそ算数・数学の仕事に携わっていますが、小学生時代は算数が好きではありませんでした。 しかし中学生の時、父からこんな話を聞いて、算数・数学の不思議に目覚めました。 半分が半分になって……をくり返すのに、なぜ0になる? 例えば、ゴールと猫との間が最初16mだったとします。 猫が進むと、ゴールまでの距離がどんどん縮んでいきますよね? 半分進むと残り8m、その残りをさらに半分進むと残り4m、同じようにまた半分進むと残り2m、…… 16÷2=8、8÷2=4、4÷2=2、……★ ここでお気づきの方もいらっしゃるかもしれませんが、 「●÷2=0」となるのは●=0のときなのに、この★の式を同じように続けていっても、0にはならないのです。 なのに、猫はゴールに到着します。 不思議だと思いませんか? 私はこの話を聞いて数学への興味が高まり、理数科への進学を決めました。 同じ数字をくりかえす? 算数・数学についての興味深い話を、算数・数学の学参編集担当にも聞いてみました! そのなかから2つ紹介しますね。 電卓を用意して、「1÷7=」を入力してみてください。(もちろん、筆算でもOK) 1÷7=0.142857142…… 「142857」という数字の並びが、くり返し現れてきます。 続いて、2÷7、3÷7……、6÷7も、同じように計算して、並べて書いてみてください。 よく数字を見てみると、どの計算結果にも、「142857」の数字の並びが現れています! 9の倍数でかけると…… ふたたび電卓を用意して、「12345679」に「9の倍数」をかけてみてください。 「12345679」なので、「8」は入りませんよ。 かけ算の結果に、同じ数字が並びましたね。 同じように、「×45、×54、×63、×72、×81」も計算してみてください。 どうしてこんな計算結果になるのでしょうか? 「×9」の計算をしてみると、そのからくりが少し理解できます。 まとめ いかがでしたか? 今回は3つの不思議を簡単にご紹介しましたが、算数・数学の不思議はまだまだたくさんあります! ぜひ、算数・数学の先生に聞いてみたり、本を読んだり、Web検索をしてみたりしてみてくださいね。
【2026年度最新】中学生向け 数学の問題集はどう選ぶ?目的別のおすすめ問題集9選
最終更新:2026-02-25 中学校から始まる「数学」。 高校受験に必要な重要科目ですが、世の中には色々な種類の問題集が発売されており、どうやって選んで良いか分からない、という方も多いのではないでしょうか? 正直数学が苦手。基礎的な学習から取り組みたい。 学校の数学の成績をアップさせたい。 実戦的な高校入試の数学に備えたい。 このように数学の問題集を手に取る目的は様々かと思います。 しっかり目的に合わせた問題集を選ぶことでより確実に学力UPを目指すことが出来ます。 今回の記事を読んで、数ある問題集の中から、あなたにぴったり問題集を選んでください! 目次 1.中学数学の「苦手」は問題集を使って克服しよう 2.中学数学の問題集はどう選ぶ? 3.授業の予習・復習&定期テスト対策に おすすめ問題集3選 4.レベルに合わせて、実力アップができる おすすめ問題集3選 5.高校入試にそなえる おすすめ問題集3選 6.まとめ <POINT> ・まずは目的を定めよう ・自分のレベルに合ったものを選ぼう ・学校の成績UPには教科書準拠の問題集が最適 1.中学数学の「苦手」は問題集を使って克服しよう 小学校の「算数」から中学の「数学」になりグッと難しくなります。 苦手を克服するにはどんな問題集を選べば良いのでしょうか? つまずきやすい「中学数学」 中学数学がつまずきやすい理由の一つに、小学校の算数では身近で具体的な事象を問題にして計算して答えを出す、といった学習が中心となっていたのに、中学数学ではXやYなどを使った文字式が登場し、それを図にするなど抽象的な内容を扱うため理解しにくい、といった事が挙げられます。 数学は高校入試の必須科目のひとつ 上記の通り中学数学はつまずきやすい科目ではありますが、高校入試においては必須科目の一つとなっています。 志望校合格のためにも、早めに苦手を克服して高校入試に備えたいですね。 また中学数学は高校数学の基礎となっており、苦手なまま高校に入学してしまうと、もっと難しい高校数学では学校の勉強についていくのが非常に難しくなってしまいます。 中学数学には応用力も求められる 計算がメインの小学校の算数と比べると、中学数学は公式を覚えるだけでなく「理解して応用する」といった事が求められます。 また理解した公式をどこで・どう使うのか?ということを学ぶためにも、多くの問題を解いて理解を深める必要があります。 そのためには学校の勉強だけでは不足しがちで、問題集を使ってより多くの問題に取り組むことが非常に重要なのです。 2.中学数学の問題集はどう選ぶ? では実際に問題集を選ぶためにはどんなことを考える必要があるのでしょうか。 教科書に対応しているものを選ぶ 中学校の教科書は各地域によって使っている教科書会社が異なりますが、数学の場合は教科書会社によって各単元を学習する順番や単元の名称などが異なります。 そして問題集には学校の教科書に対応しているものと、そうでないものがあります。 教科書に対応していることを「教科書準拠」と呼び、そうでないものを「標準版」を呼びます。 書店では教科書準拠と標準版で分けて陳列している書店もあるので、参考にしてください。 教科書準拠ですとお手持ちの教科書に沿った内容・順番で学習できるので、学校の勉強の予習・復習がやりやすいというメリットがあります。 定期テストで点数が上がるものを選ぶ 学校から配布される教科書をやりこみ、しっかりと理解することができれば、定期テストで60~70点は取れるようになると考えられます。 それ以上の点数を目指す場合、学校配布の教科書だけではなく学校の教科書の内容に沿った様々なパターンの問題演習を行っていく必要があります。 特に数学に関してはパターン理解が重要になってまいりますので、繰り返し問題を解くことが必要な教科です。 教科書の中身と似ている問題演習のパターンをしっかり理解することで定期テストの点数UPを目指すことができます。 これには「教科書準拠版」の問題集がおすすめです。 教科書準拠の問題集を探すなら 学習の目的に合っているものを選ぶ 問題集は色々な目的に合わせて作られています。 ですから、選ぶ際も自分がどのような目的で学習したいのか、といった点を確認してください。 苦手を克服したい、学校の成績を上げたい、高校入試の問題を解きたい、より難しい問題にチャレンジしたい、といった具合です。 自分のレベルに合わせて選ぶ 数学の問題集は学年別・レベル別になっている傾向が強く、自分自身がその学年の内容が理解できているか、基礎が理解できているか、といったことが大事です。 実際に中身を見て選ぶ 問題集は実際に書店で手に取って選ぶことを強くお勧めします。 書名や表紙に書いてある情報だけで選んでしまうと、実際には目的やレベルに合っていなかった、ということが起こりがちです。 また問題集の構成も毎日学習するもの、分野ごとにまとめて学習する物、定期テストや高校入試の模擬テストが入っているもの、など様々です。 3.授業の予習・復習&定期テスト対策に おすすめ問題集3選 まずは学校の授業の予習・復習や定期テスト対策におすすめの問題集をご紹介して行きます。 学校の勉強の全て基本となるのは教科書です。ですから、教科書準拠の問題集を選ぶのが最も効果的です。 中学教科書ワーク 数学 教科書に沿って学習していくなら、まずは「教科書ワーク」が定番です。 数学の場合「標準版」の問題集だと、学習の順番や単元名称が教科書と異なり分かりにくい場合がありますが、教科書ワークならお使いの教科書と全く同じ単元配列、単元名称なので予習・復習がやり易いです。 また教科書ワークはフルカラーの紙面で見やすく、自然と学習が進むよう工夫がされています。 基礎から応用と段階を追って構成されているので無理なく学習が進むのも特徴です。 さらに定期テスト対策問題や自動採点CBT、いつでもどこでも学習できるWEBアプリ「Newどこでもワーク」など学習をサポートする付録も充実。 教科書準拠問題集はまず教科書ワークからチェックしてください。 購入の際はお使いの教科書会社を確認することを忘れずに。 ▶シリーズページはこちら ▶ご購入はこちら 中学教科書ガイド 数学 「教科書ガイド」は教科書の内容をもれなく・くわしく・わかりやすく解説してあります。 教科書の問題の答えはもちろん、考え方やヒントも細かく掲載しているため、教科書の内容理解にぴったりです。 また定期テストは教科書の内容から出題されることも多いですが、重要項目やテストに出そうな事項がわかりやすくまとめてありますので、テスト対策にも最適です。 購入にあたってはご自身の持っている教科書会社を必ず確認しましょう。 なお、対応している教科書会社によって中学教科書ガイドの発行会社も異なりますのでご注意ください。 ▶シリーズページはこちら ▶ご購入はこちら 定期テストの攻略本 数学 学校の定期テスト対策であれば「定期テストの攻略本」がおすすめ。 こちらも教科書準拠問題集ですが、教科書ワークや教科書ガイドと違うのは、定期テストに特化した問題集、ということです。 教科書の要点がコンパクトにまとまっているので、テスト直前の学習にぴったり。 要点の内容学んだらテスト対策問題に取り組みましょう。コンピューターで取り組む自動採点CBTでも実力を試せます。 もちろん定期テストの予想問題も収録しているので、テスト本番を意識した学習にバッチリです。 付録には5分間でチェックできる赤シート付きの「5分間攻略ブック」が付いてきますから、定期テスト開始直前まで学習できるのも嬉しいですね。 ▶シリーズページはこちら ▶ご購入はこちら 4.レベルに合わせて、実力アップができる おすすめ問題集3選 数学の問題集は基礎中心で構成されているものから応用問題中心のものまで様々なレベルの問題集があります。 もし基礎が出来ていないのに難しい問題集に取り組んでも学習効果を得ることは難しいです。 また数学は1年生で得た知識を2年生、3年生と学年が上がるにつれてさらに応用されて学んでいく教科です。 例えば1年生で学習する比例・反比例・座標の理解が出来ていないのに2年生で習う一次関数の問題を解くこと出来ないでしょう。 3年生では関数の問題はさらに難しくなります。 まずは今の自分自身のレベルを把握することが大事ですが「どこがわからないか分からない」「なんとなく苦手」というようにあやふやな状態になっている場合は、まず基礎レベルの問題集から取り組むのがおすすめです。 わからないをわかるにかえる 学年別 数学 「数学が苦手」という中学生に向けて作られた超基礎レベルの問題集です。 まずは左のページの解説を読み、右ページの問題を解き、まとめのテストでテスト対策、という紙面構成になっています。 解説のページは大事なところが一目で分かるように文字とイラストで分かり易く書かれており、問題のページもヒントがたくさんあるので解きやすい工夫がされています。 大事な問題だけ厳選して掲載しているので、数学が苦手でも無理なく学習することが出来ます。 数学が苦手なら、まずは「わからないをわかるにかえる 数学」を手に取ってみてください。 ▶シリーズページはこちら ▶ご購入はこちら 完全攻略 学年別 数学 「完全攻略 学年別 数学」は高校入試の基礎固めに最適な標準版問題集です。 見開き2ページで充分な量の分かり易い解説が掲載されており、問題演習もステージ1で基本問題、ステージ2で標準問題、ステージ3で応用問題と少しずつ難しくなっていくスモールステップ形式になっているので、着実にレベルアップすることが出来ます。 また別冊解答解説もとても詳しく書いてありますので、間違えた問題もしっかり復習できます。 「定期テスト対策問題」も収録されておりテスト対策もバッチリ。 さらにWEBからダウンロードできる「完全攻略テスト」も付録もあり、充実の内容となっています。 ▶シリーズページはこちら ▶ご購入はこちら ハイクラス徹底問題集 数学 中学生向けの問題集としては最高レベルとなる問題集が「ハイクラス徹底問題集 数学」です。 レベル1の「徹底確認」では公立高校の入試を中心に標準レベルを収録、レベル2の「実力完成」では公立・私立のややレベルの高い問題を収録、レベル3の「難関攻略」では私立・国立の難関校を含むかなりレベルの高い問題を収録、といった紙面構成で、詳しい解答解説も付いて難問対策もバッチリです。 読むだけで勉強になるコーナー解説も充実。他の問題集では物足りない、学年トップクラスを取りたい、難関高校の入試を突破したいという人にピッタリの問題集です。 ▶シリーズページはこちら ▶ご購入はこちら 5.高校入試に備える おすすめ問題集3選 最後に高校入試に備えるための最適な問題集をご紹介します。 高校入試対策問題集も数多く発売されていますが、最近は各都道府県で今までになかったような新しい傾向の入試問題が出題されるようになっており、古い問題集だと対策が難しい場合も多くなって来ています。 以下でご紹介するような最近発売された、または最近改訂された問題集を選ぶようにしてください。 わからないをわかるにかえる 高校入試 数学 前述の超基礎問題集「わからないをわかるにかえる」シリーズの高校入試版です。 高校入試は中学3年間で学んだ学習内容から出題されるわけですが、問題を解く際に重要となるのはやはり基礎学習です。 実際に出題された入試問題を解きながら理解を深めることが出来るのが特徴で、もし高校入試対策に取り組む時に数学が苦手だなと感じたら、まずはこの「わからないをわかるにかえる 高校入試 数学」で3年間の基礎をしっかり確認するところから始めましょう。 ▶シリーズページはこちら ▶ご購入はこちら コーチと入試対策 「8日間完成 中学1・2年の総まとめ」 「10日間完成 中学3年間の総仕上げ」 数学 こちらは2022年秋に発売されたばかりの新シリーズ「コーチと入試対策」の問題集で、短い期間で効率よく入試対策が出来るのが最大の特徴です。 夏休みや冬休みといった限られた時間で一気に学習したい人におすすめ。 つまずきやすい部分もコーチの丁寧な解説ですっきり解消できます。 付録の応援日めくりでモチベーションもアップ。 「8日間完成 中学1・2年の総まとめ」は3年生になる前や夏休みの復習に最適で「10日間完成 中学3年間の総仕上げ」は受験直前の最終確認に最適です。 目的に合わせて選んでください。 ▶シリーズページはこちら ▶ご購入はこちら 完全攻略 「中1・2の総復習」「3年間の総仕上げ」 数学 前述の「完全攻略シリーズ」の入試対策版です。 高校入試の出題範囲の7割は中1・2年の学習内容と言われており、高校入試を突破するにはまず「完全攻略 1・2年の総復習」で復習しましょう。 要点のまとめと基本問題を繰り返し学習し、実際の入試問題で構成された「実戦テスト」で実力をUP。 巻末の「総合テスト」で1・2年の学習内容の理解度を確認します。 そして高校入試の仕上げは「完全攻略 3年間の総仕上げ」が最適。 要点のまとめや基本問題、実戦テストはもちろん、テーマ別のより実戦的な問題を解くことでワンランク上の実力をつけることが出来ます。 最後は「模擬テスト」で入試対策は完璧です。 ▶シリーズページはこちら ▶ご購入はこちら 6.まとめ 中学数学の問題集と言っても様々なものがありますが、自分自身にぴったり合った問題集を選べば着実に学力をUPすることが出来ます。 中学で最もつまずきやすい教科と言われる数学を、文理の問題集と一緒に攻略して行きましょう!
0って実はこわ~い数字って本当? 数字の不思議!
ハッピーハロウィン! 皆さん、今日は10月31日、ハロウィン当日ですね!みなさん、おかしの準備や、仮装の準備はできましたか? そんなハロウィンにピッタリな、こわ~い数字について、皆さんにご紹介していきます。 怖い数字とは? 誰もが震え上がる怖い数字とは 0 です!! いやいや、0の何が怖いんだって思いますよね。普通に計算するときに使いますし、日常でも特に疑問に思うことなく見かける数字です。しかし、中世ヨーロッパでは0は悪魔の数字とも呼ばれていました。 0はどうして生まれたのか 0ができたのは、他の数字よりもずっと後です。昔のヨーロッパではローマ数字と呼ばれるⅠ、Ⅱ、Ⅲ,Ⅳという数字が使われていました。 かっこ良く見えるこの数字の表し方、数が大きくなればなるほど書いて表すのが大変なんです。 例えば数字の12はローマ数字でⅫと表します。 まだ、簡単ですよね。もっと大きな数字をローマ数字で表してみましょう! このように、今はたった4文字で表せた数でも、昔は何文字も使う必要がありました。とっても大変ですね! そんななか、インドの数学者によって、「何もない」ということを表す記号として0が生まれます。 当時はまだ数字と認められておらず、0というただの記号でしたが、今まで「何もない」という状態を表すすべを持っていなかった中世ヨーロッパの人たちはとても驚きました。また、0が生まれたことにより、今私たちが使っているような、【1,2,3,4,5,6,7,8,9,10】といういわゆる10進法と呼ばれる数字の表し方が誕生しました。 なぜ悪魔の数字と呼ばれるようになったのか 簡単に大きな数字を表せるようにしてくれた便利な数字「0」ですが、なぜ悪魔の数字と呼ばれるようになってしまったのでしょうか? それは0が、何もないという状態を作ってしまうからです。 例えば 上の計算式のように、どんなに、大きな数字でも0をかけてしまえば、0になります。 算数の授業でかけ算を習った人にとってはあたりまえのことですよね。 しかし、先ほど書いたように中世のヨーロッパの人たちは「何もない」という状態を表す方法すら持っていなかったので、「0」という数字をとても恐ろしく感じました。 そのため、昔の人々は「0」を「悪魔の数字」と呼びました。 そして、もう一つ「悪魔の数字」と呼ばれるようになった理由があります。それは、0は数学のルールを壊してしまうということです。 皆さん授業で、「0で割ってはいけない」というルールを勉強しませんでしたか?実は、0で割り算をしてしまうと、計算が成り立たなくなってしまうんです。 まず、0=0と定義します。これは当然のことですよね。0は0なので。 上の式が正しいとすると、 つまり、1×0=2×0という式が成り立ちます。 これをそれぞれ0で割ってみると、 0が消えるので、1=2 というありえない計算式が成り立ってしまいます。 また、今回は上の計算式の例をご紹介しましたが、0で割ってしまうと他の計算のルールも破壊されてしまう可能性があります。 そんなルールを壊してしまう0は中世ヨーロッパの人たちにとって、悪魔と同じくらい恐ろしいものだったのです。 まとめ 今では普通に使用されている「0」ですが、実は計算を狂わしてしまうこわ~い数字でした!筆者も何かの本で、この「0」は「悪魔の数字」ということを知ったのですが、今まで普通に計算で0を使ってきたのでまさかそんな風に呼ばれていたなんて!ととても驚きました。 普段何気なく使っている、計算方法や数字でもおもしろい話が隠れているかもしれません、是非探してみてください。
中学生1年生 数学の問題集の選び方
算数は小学校で終わり、中学校1年生から始まる「数学」は高校受験に必要な重要科目ですね。 しかし算数よりも難易度が高いことでちょっと苦手、定期テストで良い点数を取りたいけれど、どのような対策をして良いかわからない、なんて人も多いのでは多いのではないでしょうか? 今回は中1数学の問題集の選び方についてまとめました。 この春中学1年生になった方には特に知って頂きたいので、是非最後までお読みください! 目次 1.中学1年生におすすめの数学問題集の選び方 ・適切な難易度を選ぶ ・問題の体裁やレイアウトに注目する ・解答解説の充実度を確認する ・口コミをチェックする 2.中1 数学問題集の種類・特徴とおすすめの問題集 ・教科書準拠問題集なら、「中学教科書ワーク 数学1年」 ・基礎問題集なら、「わからないをわかるにかえる 中1数学」 ・標準レベルの問題集なら、「完全攻略 中1数学」 ・ハイレベル問題集なら、「ハイクラス徹底問題集 中1数学」 3.まとめ 1.中学1年生のおすすめの数学問題集の選び方 中1数学の問題集といっても色々な問題集が出版されています。 ここでは目的別の選び方や選ぶ時のポイントを紹介します。 適切な難易度を選ぶ 例えば中1の数学で最初に習うことの多い「正負の数」ですと、小学生の算数では習わなかった0より小さい数である「負の数」が登場します。 マイナスの数という考え方は抽象的で分かりにくいため、中1なってから最初に苦手意識を持つ人が多い学習内容かと思います。 ですので、まずは購入する前に問題集の「正負の数」のような数学の基本となる単元を試し読みして、自分でしっかり理解できるかどうかを確認しましょう。 ちょっと苦手意識のある人は解説のページが充実していて問題数が厳選されている易しめの問題集を、最初から問題を解いて力を付けたい人は実戦的なハイレベル問題集を選ぶのも良いでしょう。 問題の体裁やレイアウトに注目する 一口に問題集といっても紙面の体裁やレイアウトはそれぞれ異なります。 学習する前にその単元がわかりやすく解説されているもの、まとめ部分の空欄を埋めて問題に慣れてから練習問題に取り組むもの、最初から入試問題などをどんどん解いていくものなど様々です。 また文字の大きさやフルカラーかどうかなども、学習のしやすさに関係してきます。 漫画形式やキャラクターなどが丁寧に解説してくれるタイプの問題集もありますので、好みに合わせて選んでください。 解答解説の充実度を確認する 問題集は問題を解くページだけでなく、解答解説のページが非常に重要です。 例えば中1で初めて出てくる方程式では、算数には出てこなかった記号が出てきて、混乱する人も多いのではないでしょうか。 問題を解く際にどうやってその答えに辿り着いたのか、といった答え合わせの際に重要になってきますので、途中式が載っており詳しい解説がついていると良いでしょう。 口コミをチェックする 最近はネット書店でも多くの参考書が販売しています。 書店では実際の紙面が見られることが大きなメリットとなりますが、一方でネット書店であれば実際にその参考書を購入した人の使用感などがわかることが多いです。 中学1年生となると自分で問題集を選ぶ、という人も増えてくると思いますので一度はチェックしたいですね。 もちろん、口コミに書いてあることが全て正しいとは限りませんので、実際に購入する際は必ず自分で紙面を確認しましょう。 2.中1 数学問題集の種類・特徴とおすすめの問題集 それでは次に中1数学問題集の種類と特徴、おすすめの問題集を見ていきましょう。 教科書準拠問題集なら、「中学教科書ワーク 数学1年」 教科書準拠問題集は教科書の内容、順番に沿って作ってあるので、学校の授業に合わせて使うことができます。 実は教科書は学校や地域によって使用している教科書が異なるため、中1といっても全国の中学校で同じように授業が進むわけではありません。 しかし教科書準拠問題集であれば、通っている学校で使っている教科に合わせて予習復習できるため、無理なく確実に学習できます。 中学といえば「定期テスト」が重要になってきますが、定期テストも教科書範囲から出題されることが多いため、テスト対策としても有効です。 教科書準拠でおすすめの問題集は何といっても定番の「中学教科書ワーク 数学1年」です。 教科書ワークはお使いの教科書と全く同じ単元配列、単元名称なので、中1数学の予習・復習がとてもやりやすいことが最大のメリットです。 フルカラーの紙面で見やすく、また基礎から応用と段階を追って構成されているので無理なく学習が進むのも使いやすいポイント。 もちろん中学の内申点にも大きく影響する「定期テスト」の対策問題やホームページテスト、スマホアプリ「どこでもワーク」など学習をサポートする付録も充実しています。 なお、購入の際はお使いの教科書会社を必ず確認するようにしてください。 ▶シリーズページはこちら ▶ご購入はこちら 基礎問題集なら、「わからないをわかるにかえる 中1数学」 少し数学が苦手、といった人やまずはしっかり基礎力を鍛えたい、という人におすすめなのは、基礎問題集です。 まとめページの丁寧な解説や、カラフルで見やすい紙面が特徴です。 問題数も厳選されており難しい応用問題は少ない傾向にあるので、中1で良くあるつまずきが起きないように工夫して作られています。 おすすめは「わからないをわかるにかえる 中1数学」です。 ①左ページの解説を読み ②右ページの問題を解き ③まとめのテストでテスト対策 という紙面構成で、解説のページは大事なところが一目でわかるように文字とイラストでわかりやすく書かれています。 つまずきやすいポイントにはヒントが掲載されているなど、ちょっと苦手な人でも解きやすい作りになっています。 ▶シリーズページはこちら ▶ご購入はこちら 標準レベルの問題集なら「完全攻略 中1数学」 教科書レベルの問題をもっと演習したい、教科書よりもう少しだけ難しい問題にも挑戦したいという人におすすめなのが標準レベルの問題集です。 「完全攻略 中1数学」は定期テストと対策と高校入試の基礎固めに最適の1冊です。 例題で解き方を学んだあと、「基本問題」「標準問題」「実戦問題」と段階別の構成で無理なくステップアップできます。 「定期テスト対策問題」や「章末仕上げ問題」もあります。 解答・解説は、問題の解き方、考え方、注意点などを詳しく丁寧に解説しています。 ▶シリーズページはこちら ▶ご購入はこちら ハイレベル問題集なら、「ハイクラス徹底問題集 中1数学」 教科書のレベルでは物足りない、早めに実戦的な応用問題に取り組みたい、という人はハイレベル系の問題集にチャレンジするのがいいでしょう。 近年、高校入試の問題も資料の読み解き問題や記述式の解答が増えているといわれており、多くの応用問題に早めに取り組んでおくことで高校入試や、それ以降の学習のアドバンテージを作ることも大事です。 そこで是非手に取って頂きたいのが「ハイクラス徹底問題集 中1数学」」です。 レベル1「徹底確認」:公立高校の入試を中心に標準レベルの問題 レベル2「実力完成」:公立・私立のややレベルの高い問題 レベル3「難関攻略」:私立・国立の難関校を含むかなりレベルの高い問題 というように、段階的に力を付けることができる紙面構成になっています。 解答解説も非常に詳細に掲載されているため、難問対策もバッチリ理解。 ちょっと他の問題集では物足りない、中1では成績トップを狙いたい、そんな人におすすめの問題集です。 ▶シリーズページはこちら ▶ご購入はこちら 3.まとめ いかがでしたでしょうか。 中学1年生の数学はつまずきやすい科目ではありますが、高校入試においては必須科目の一つです。 将来に向けた志望校合格のためにも、苦手にしたくない・または早めに苦手を克服したい教科ですね。 しっかりと学習のアドバンテージを作っておくことは、充実した中学校生活を送るためにも大事になってきます。 さらに、中学数学は高校数学の基礎となります! もっと難しい高校数学に対応するためにも、中1の数学から着実に理解して学習を進めましょう。
アゲモノ【第1回】「三平方の定理」
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 問題 スーパーマーケットで揚げ物を選んでいるとき、トングとアジフライの間に直角三角形が見えることが気になってきた。 次の三角形ABCについて、辺BCの長さを求めなさい。 ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① 三平方の定理を使ってみよう。 三平方の定理ってなんだっけ?となったらヒント2へ 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② 三平方の定理は 直角三角形において、斜辺(直角と向かい合う辺)以外の2つの辺の長さをそれぞれ2乗して足すと、斜辺の長さの2乗と等しくなる、 という公式。 ちなみに、2乗とはその数を2回かけ算すること。2の2乗=2×2=42の3乗=2×2×2=8 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 解答 5cm 三平方の定理によると、直角三角形において、a²+b²=c² が成り立つ。 問いの直角三角形ABCについてa=BC、b=AB、c=CAとして、三平方の定理を使うことができる。 a²+b²=c² ⇒ BC²+AB²=CA² AB=12、CA=13なので、BC²+12²=13² これを計算していくと、BC²=13²-12²BC²=169-144BC²=25 BCは2乗して25になる数字なので、5または-5があてはまるが、三角形の辺の長さが負の数や0になることはありえない(BC>0) よって、BC=5 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら
アゲモノ【第6回】「円の面積」
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 質問 この図形は何に見えますか? ▼選択してください▼ エビフライ トンカツ からあげ 本当にそうでしょうか? 戻る▲ そう!エビフライに見えますね。 では問題 このエビフライのように見える図形の面積を求めなさい。円周率はπとする。 ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① 半径rの円の面積は、πr² また、半径r、中心角a°のおうぎ形の面積は、πr²×a/360 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② パズルのようにぴったりはめると…?しっぽの部分を足すのも忘れずに。 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 解答 36πcm² 小さい半円を図のように移動させると、 衣の部分を大きな円の半分と見なすことができます。 この大きな円の半径は8cmなので、衣の面積は、π×8²×1/2=32π(cm²)です。 しっぽの部分を忘れずに足します。この部分は、半径4cmの円の1/4なので、面積は、π×4²×1/4=4π(cm²)となります。 求める面積は、32π+4π=36πより、36πcm² です。 ★ちなみに★ πは「周囲(perimeter)」の意味を持つギリシャ語 περίμετρος (ペリメトロス) の頭文字です。 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら ④旅するワーク 「地球の歩き方」とコラボした新シリーズ! 世界の国々の地理・歴史について、旅行気分で学び直してみませんか? 「知らなかった!」となる豆知識もたっぷりで、大人でも楽しめます! ▲地球の歩き方ライターによるコラムも豊富で読み応え抜群! ▶シリーズページはこちら ▶ご購入はこちら
日々の積み重ねが大切!「算数ドリル」で算数を得意教科にしましょう
算数でドリル学習が効果的な理由 小学校では、「計算ドリルの●ページを解きましょう」と宿題が出ることが多いですね。 ドリルを解くことは、学習したことの定着にとても大切です。 その理由を見てみましょう! 繰り返すことで解き方が定着するから ドリルでは、同じ学習事項を様々な形式で解きます。 しっかりと取り組むことで学習内容が自然と定着し、より速く、より正確に解くことができるようになるのです。 「教科書ドリル」では、同じ学習事項をおもて・うらの両面で解きます。 答え合わせ、間違い直しをする過程でしっかりと定着させることができます! 体系的で学習計画が立てやすいから ドリルは、「じっくり時間をかけて理解をする」よりも、 「理解したことをアウトプットして定着させる」ことに重きを置いていることが多いです。 そのため、1回あたりにかける時間はそれほど多くなく、日々の生活に取り入れやすいです。 平日は、宿題にプラスしてドリルを取り入れ、休日はワークをじっくり解く…といった学習計画を立ててみましょう。 「教科書ドリル」のように、巻末に学習記録をつけられるドリルもあります。 毎日取り組むことで学習が習慣化するから 取り組む学習内容によって難易度が大きく異なっていたり、学習時間が日によって違っていたりするとなかなか慣れず、 勉強に抵抗を感じてしまい続きません。 しかし、ドリル学習であれば同じ難易度・同じ学習時間に設定されていることが多いため、 毎日どのくらいの時間取り組むべきかを把握しやすく、続けやすいです。 習慣づけをすることができたら、1日に取り組む量を少し増やす、レベルを少し上げる、などの工夫をしてみましょう。 効果的な算数ドリルの選び方 ドリル学習は、毎日コツコツ続けて学力を定着するのにぴったりです。 算数は地道な努力を積み重ねることが大切な教科なので、ドリル学習と相性抜群! 書店に行くと、たくさんの種類のドリルがずらりと並んでいます。 お子さまひとりひとりに合ったドリルの選び方を見ていきましょう。 子供のレベルに合ったものを選ぶ ドリルは、1枚あたりに取り組む量や1枚あたりのレベルがしっかりと設定されています。 算数が得意なお子さまであれば、「トップ」「ハイレベル」などの名前が付いた比較的レベルの高いドリルに挑戦してみましょう。 算数がニガテでどうしても抵抗感がある……。というお子さまであれば、 まずはお菓子やキャラクターがふんだんに使われていて、問題数の少ないドリルから始めてみましょう。 答え合わせがしやすいものを選ぶ ドリルで一番大切なのは、答え合わせと間違い直しです。慣れないうちは保護者の方のサポートが必要ですが、 理想はお子さま1人で答え合わせと間違い直しができることです! ドリル学習が初めて!という方は、縮刷解答になっているドリルを選んでみましょう。 問題がそのまま印刷されており、答えが載っているので答え合わせがしやすくなっています。 解説が充実しているものを選ぶ 間違い直しをするとき、途中式や解説の記載が少ない解答・解説のドリルを選んでしまうと、 どこで間違えたか、なぜ間違えたかが分からなくなってしまいます。 特に、算数のニガテを克服したい!という目標があるご家庭では、 しっかりと解説が充実したドリルを選ぶことが大切です。 苦手なところは分野別ドリルで補う 算数は、「計算」や「図形」といった分野別になっています。 お子さまが苦手とする領域をしっかりと把握し、学年をさかのぼってみたり、 予習をして授業についていけるようにしたり、というケアを行うことで克服できる可能性がグッとアップします! 「教科書ドリル」や「できる!!がふえる↑ドリル」は分野別に分かれているので、書店でお子さまとお手に取ってみてください。 効果的な算数ドリルの学習方法 毎日取り組むドリルを選ぶことができたら、いよいよ実践です。 最後までしっかりと解き切ることができるコツをご紹介します! 毎日ちょっとずつ取り組む 2日に1回、3日に1回まとめて……。としてしまうと、いつ取り組むのか忘れてしまい続かなくなってしまいます。 「毎日決まった時間に、1枚だけ解く」から始めてみましょう。 習慣化できるようになってきたら、「1日2枚、朝晩1枚ずつ」といったルールを追加してみましょう。 その日のうちに答え合わせをする 解きっぱなしでは、なかなか力が付きません! なので、10~15分と時間を決めて解いた後は、サッと答え合わせまでしてしまいましょう。 なるべく、解いた感覚を忘れないうちにすぐに答え合わせをすることがおすすめです。 間違えたところの復習をする 間違えてしまった箇所は、計算ミスなのか、理解が不足しているのか……。といった原因を分析して、解き直すようにしましょう。 計算ミスの場合は、少し演習量を増やす、ゆっくり丁寧に解くことを意識する、などの対策が考えられます。 理解が不足している場合は、教科書やワークで解き方をしっかりと確認してからドリル演習を再開するようにしましょう。 「間違い」は次につながる大事なステップです。しっかりと復習しましょう! 楽しくドリル学習を続けるコツ ドリル学習を続けるためには、お子さまのモチベーションが続くことがなにより大切です。 日々取り組むものなので、保護者の方が強制するのではなく、お子さまが自然と自ら机に向かうような環境づくりをしましょう。 子供が気にいったドリルを選ぶ まず大切なのは、実際に親子で書店に行き手に取って、お子さま自身がやる気になるドリルを選ぶことです。 保護者の方は、お子さまのニガテや現在のレベルをある程度把握して、現在のお子さまの状況に合ったものを勧めるサポートを行いましょう。 進捗や達成度を見える化 お気に入りのドリルを選び購入することができたら、まずは解いてみましょう。 達成感が感じられるよう親子で一緒に記録をつけたり、シールを貼ってみたりといった工夫をしましょう。 「おかしなドリル」のように、ドリル自体にシールや達成シートが付属しているものもあります! ごほうびでモチベーションアップ 「毎日ドリルを続けることができるようになった」、「学校のカラーテストで点数が上がった」といった嬉しい変化は見逃さず、 しっかりと褒めてのばすことが大切です! 「まずは1週間ドリルを毎日続ける」、「カラーテストで90点以上取る」といった目標をお子さまと一緒に決めて、 達成した時にもご褒美を用意しましょう。 「おかしなドリル」では、クラフト工作ができます。 また親子でお菓子作りをするレシピが掲載されていたりするので、 設定した目標が達成できたときにご褒美として活用するのもおすすめです! おすすめの算数ドリル 具体的に、お子さまの状況に合わせておすすめのドリルをご紹介します! ドリルによって、サイズ、問題量が様々です。 また、1枚ずつはぎとれるドリル、シールやボードなど付録がついたドリルなど、そのドリルならではの特長があるドリルもあります。 特長を押さえたうえで、ぜひじっくり比較してお選びください! 小学教科書ドリル 国語・算数が教科書準拠になっています。 教科書の単元名やページ数が各ページに掲載されているので、理解が不足している部分は教科書を確認して復習することができます。 ▶シリーズページはこちら ▶低学年ご購入はこちら ▶高学年ご購入はこちら できる‼がふえる↑ドリル 細かく分野別に分かれているのが特長です。 お子さまの得意・不得意に対し、ピンポイントでアプローチできます。予習・復習におすすめです。 ▶シリーズページはこちら ▶ご購入はこちら おかしなドリル 算数のニガテを自然と克服する工夫が詰まった、小学生低学年用のドリルです。 明治のおかしがたくさん登場するので、ワクワクしながら解き進めることができます。 ボードやシールなどの付録をしっかり活用して、小さいお子さまでも最後まで解き切ることができる構成になっています。 ▶シリーズページはこちら ▶ご購入はこちら ハイレベル算数ドリル 算数の得意をさらにのばすことができるドリルです。 オールカラーながら、難易度の高い問題が多く掲載されておりステップアップ式で抵抗感なくすすめることができます。 ▶シリーズページはこちら ▶ご購入はこちら
小学生でもわかる!パーセント計算のやり方とコツ
もくじ はじめに パーセントとは? パーセント計算の基本ルール 割引や増加・減少とパーセント計算 パーセントの計算をもっと楽しくするコツ 計算が得意になる! おすすめ問題集 まとめ はじめに 「この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は…」 「水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何%かな?」 「この服、4500円だけど30%オフになっているよ!いくらになるのかな?」 私たちの生活の中には、パーセント(%)という言葉がたくさん出てきます。 パーセントを理解すると、身の回りのことがよくわかるようになります。 この記事では、小学生のみなさんにもわかりやすいように、パーセントの基本的な考え方、計算方法、ちょっとしたコツなどを紹介します。 パーセントの世界を一緒に探検してみましょう! パーセントの計算ができる文理のドリルシリーズはこちら! できる!!がふえる↑ドリル ハイレベル算数ドリル 小学教科書ドリル パーセントとは? ◆パーセントの意味 普段の生活の中でパーセント(%)という記号をよく見かけますよね。 これは、 「全体を100としたときにどのくらいあるか」 を表す記号です。 「%」を使って表す割合を、百分率といいます。 全体を100(百)としているので百分率です。 たとえば、全体で100人いる中で、20人がめがねをかけているとき、めがねをかけている人は「20%」になります。 全体を100として考えることで、全体の数が半端な数であっても、どのくらいあるかわかりやすくなります。 ◆割合、歩合、百分率の関係 百分率と合わせて、割合や歩合という言葉も使われます。 これは、全体を何にするかで使い分けます。 ・割合 → 全体を1としたときにどのくらいあるか。 単位はつけません。 ・歩合 → 全体を10としたときにどのくらいあるか。 単位は割(わり)、分(ぶ)、厘(りん)などを使います。 ・百分率 → 全体を100としたときにどのくらいあるか。 単位は%です。 割合を10倍すると歩合、割合を100倍すると百分率になります。 具体例で確認してみましょう。 全体で100人いる中で、20人がめがねをかけているとき、 ・割合 → 0.2 (20÷100=0.2) ・歩合 → 2割 (20÷100×10=2) ・百分率 → 20% (20÷100×100=20) となります。 3つの関係を表にまとめると、関係がわかりやすくなります。 歩合が使われることは減っていますが、野球の打率を表すときに使われます。 例:文理野球部4番バッターの今年の打率は、3割ちょうどでした。 この場合、このバッターは、10打席中3打席ヒットやホームランを打つと考えられます。 パーセント計算の基本ルール ◆「○○の□□%」を計算する方法 ここからは、テストでもよく出る問題の解き方を、パターン別に解説します。 解き方を確認したら、練習問題にもチャレンジしてみましょう! 例題 400円の20%は? 解き方・答え 計算するときは、百分率を割合に直します。 20% → 0.2 (20÷100=0.2) 400×0.2=80(円) 20のまま計算しないよう注意しましょう。 では、練習問題です! 練習問題 ★次の計算をしましょう。 1.800gの20%は? 2.600Lの30%は? 3.700人の15%は? 4.この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は… ↑4は、はじめにで紹介した問題です! 解き方・答え 1.20% → 0.2 800×0.2=160(g) 2.30% → 0.3 600×0.3=180(L) 3.15% → 0.15 700×0.15=105(人) 4.10% → 0.1 500×0.1=50(mL) パーセントを使って計算するときは、百分率を割合に直すことを忘れないようにしましょう。 ◆「□□は○○の何%?」を計算する方法 次は、割合を計算してからパーセントを求める問題です。 例題 80円は400円の何%? 解き方・答え まず、割合を求めます。 80÷400=0.2 何%か求めるので、100をかけて百分率に直しましょう。 0.2×100=20(%) では、練習してみましょう! 練習問題 ★次の計算をしましょう。 1.50gは200gの何%? 2.48Lは80Lの何%? 3.150人は1250人の何%? 4.水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何%かな? 解き方・答え 1.50÷200=0.25 0.25×100=25(%) 2.48÷80=0.6 0.6×100=60(%) 3.150÷1250=0.12 0.12×100=12(%) 4.6÷300=0.02 0.02×100=2(%) 百分率(パーセント)で答えるので、100をかけて百分率に直すことに注意しましょう。 割引や増加・減少とパーセント計算 ◆割引とパーセント お店で買い物をするときに、「30%オフ!」というPOPを見かけることはありませんか? これは、元の値段から30%安くなることを表しています。 割引されるときのパーセントの計算を確認しましょう! 例題 5000円の服が40%オフで売られています。支払う金額はいくらですか? 解き方・答え 40%が0.4であることに注意して、まずは安くなる金額を求めます。 5000×0.4=2000(円) 次に、支払う金額を求めます。 5000-2000=3000(円) では、練習してみましょう。 練習問題 ★次の問題に答えましょう。 1.800円のお菓子が15%オフで売られています。支払う金額はいくらですか? 2.2500円の商品が20%オフになっています。支払う金額はいくらですか? 3.定価12000円の自転車が35%オフで売られています。支払う金額はいくらですか? 4.この服、4500円だけど30%オフになっているよ!いくらになるのかな? 解き方・答え 1.800×0.15=120(円) 800-120=680(円) 2.2500×0.2=500(円) 2500-500=2000(円) 3.12000×0.35=4200(円) 12000-4200=7800(円) 4.4500×0.3=1350(円) 4500-1350=3150(円) ◆増える・減るときのパーセント 増えたり減ったりするときにもパーセントは使われます。 例題 タケルさんの今回のテストの点数は、前のテストの点の80点より15%増えました。 今回のテストは何点でしたか? 解き方・答え まず、増えた点数を求めます。 80×0.15=12(点) 次に、今回の点数を求めます。 80+12=92(点) では、練習問題です! 練習問題 ★次の問題に答えましょう。 1.ユイさんの身長は、1年前に150cmでしたが、この1年で5%伸びました。今の身長は何cmですか? 2.A地域の人口は、昨年10000人でしたが、今年は2%減りました。A地域の今年の人口は何人ですか? 3.お父さんの体重は60kgでしたが、ダイエットをして10%減らしました。ダイエット後の体重は何kgですか? 解き方・答え 1.150×0.05=7.5(cm) 150+7.5=157.5(cm) 2.10000×0.02=200(人) 10000-200=9800(人) 3.60×0.1=6(kg) 60-6=54(kg) より多くの問題を解きたい方はこちら! できるが!!ふえる↑ドリル ハイレベル算数ドリル 小学教科書ドリル パーセントの計算をもっと楽しくするコツ ◆暗算のちょっとしたテクニック ここからは、知っていると便利なテクニックを紹介します。 よく出るパーセントの計算方法を覚えておくと、暗算で答えが出せるようになることがあります。 ・10% → 元の数を10でわるのと同じ! 例:290円の10%は? 290÷10=29(円) ・50% → 元の数を2でわるのと同じ! (元の数の半分!) 例:800個の50%は? 800÷2=400(個) ・25% → 元の数を4でわるのと同じ! (元の数の4分の1!) 例:200ページの25%は? 200÷4=50(ページ) ・20% → 元の数を5でわるのと同じ! 例:500mLの20%は? 500÷5=100(mL) これらのテクニックを覚えておくと、暗算できることがあります。 ◆クイズでパーセントをマスターしよう! ここまで学習してきたパーセントの計算を使って、クイズに答えてみましょう。 問題 ★次の問題に答えましょう。 1.定価1000円のものが60%オフで売られています。 財布に500円しかないとき、この商品を買える?買えない? 2.50点満点のテストの結果が40点でした。90%正解したことになる? 3.果汁20%の飲み物を2本買って混ぜたら、果汁は40%になる? 4.450円の80%と、700円の50%では、どちらが安い? 解き方・答え 1.1000×0.6=600(円) 1000-600=400(円) 500円あるので買えます。 答え 買える。 2.40÷50=0.8 0.8 → 80% 答え 90%正解したことにはならない。 3.果汁20%の飲み物を何本混ぜても、果汁は20%のままです。 答え 果汁40%にはならない。 4.450×0.8=360(円) 700×0.5=350(円) 答え 700円の50%の方が安い。 計算が得意になる! おすすめ問題集 文理の書籍には、計算練習ができるものがたくさんありますので紹介します。 今回紹介したパーセントの計算以外の計算問題もたくさんあります。 計算力をつけるには問題をたくさん解くことが一番! 力をつけたい方はぜひチャレンジしてみてください。 ※パーセントの問題は、小学5年生で詳しく学習します。 パーセントの問題を練習したい方は、小学5年生の書籍をご利用ください。 ◆小学教科書ワーク 「算数」 教科書に完全対応しているから、学校の授業に合わせて使いやすい! 計算練習ノート、ポスター、動画、CBTなど付属品も充実! 全教科書に対応した「数と計算」「文章題・図形」シリーズも用意しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆小学教科書ドリル 「算数」 1回10分で終わるドリルだから、習い事など忙しくても続けやすい! 基本・確認の2ステップで、無理なく力がつきます! 計算問題に特化した「計算編」文章題や図形問題に特化した「文章題、数・量・図形」シリーズも用意しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆できる!!ふえる↑ドリル 1枚ずつはがして使えるから、学習しやすい! 「計算」「文章題」「数・量・図形」「時こくと時間」など、分野別のシリーズが充実しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆ハイレベル算数ドリル 3段階構成で取り組みやすい! 詳しい回答解説で、学習をサポート! ▶シリーズページはこちら ▶ご購入はこちら まとめ 今回の記事では、パーセントの基本的な意味から、計算の仕方、そしてちょっとしたコツまでを解説してきました。 パーセントは、私たちの身の回りの色々なところで使われています。 色々な問題にチャレンジして、パーセントマスターを目指してくださいね!
中学数学の公式をわかりやすくまとめます!高校入試にも役立つ完全ガイド
もくじ はじめに 中学数学で覚えるべき公式とは? 高校入試で役立つ公式 「なぜそうなるか」から数学公式を理解する 覚え方・使いこなし練習 おすすめの学習教材 まとめ はじめに 「数学の公式って、たくさんあって覚えきれないな…」 「高校入試に向けて、どの公式をしっかり押さえておけばいいんだろう?」 そんな悩みを解消するために、今回は中学数学で学ぶ公式を解説します! 公式を「知る」から「使える」に変えるための完全ガイド、ぜひ最後まで読んでみてくださいね! 中学数学で覚えるべき公式とは? 中学3年間で学習する数学は、主に計算(方程式)、関数、図形の3つの分野に分類できます。 ※データの活用もありますが、今回は公式ということで省略します。 一見するとバラバラに見えるかもしれませんが、実はどれも深いところでつながっています。 学年ごとに確認しましょう。 中1で習う数学公式のポイント 中学1年生になると、算数から数学に教科名が変更され、本格的な数学の学習が始まります。 中学1年生で学習する公式は、この先の数学の土台になりますのでしっかり理解しましょう。 ◆ 正の数・負の数【計算】 四則演算(たし算、ひき算、かけ算、わり算)は、符号ミスに注意することが大切です。 符号の関係を公式としてまとめておくと便利です。 ◆ 文字式【計算】 分配法則は、今後の計算の基本になりますのでここで理解しておきましょう。 割合や速さの関係も、文章題を解く上で大切です。こちらは小学校での学習内容になりますが押さえておきましょう。 ◆ 1次方程式【計算】 等式の性質が方程式を解くときの基本になります。移項するときは符号に注意しましょう。 ◆ 比例・反比例【関数】 関係式を公式として整理しましょう。座標の読み取り方も重要です。 ◆ 平面図形・空間図形【図形】 おうぎ形の面積、立体の体積を公式として覚えておきましょう。 おうぎ形は円の一部分だとイメージすると、計算するときに式を思い出しやすくなります。 中2で習う数学公式のポイント 中学2年生では、さらに一歩進んだ内容を学習します。 図形の単元で証明を学習し、ものごとを順序だてて説明する力を養います。 図形に関する公式(定義や定理)が増えますので、正確に理解する力が求められます。 ◆ 1次関数【関数】 y=ax+b の形と式の意味、変化の割合などを覚えましょう。高校入試や定期テストでは、図形問題に応用されることも多いです。 ◆ 平行と合同【図形】 平行線と角の関係や、多角形の内角の和・外角の和は、入試の図形問題を解く際にも重要な内容です。 三角形の合同条件は、証明問題を解く際、数多く出てきます。 ◆ 特別な四角形【図形】 平行四辺形、長方形、ひし形、正方形の定義や性質は、小学校で学習した内容でもあります。 中学2年生では、定義、定理として再確認します。 中3で習う数学公式のポイント 中学3年生で学習する公式は、高校入試に直結する重要なものが多くあります。 特に平方根、2次方程式、相似、円、三平方の定理は、入試の頻出単元として強調しておきたいポイントです。 ◆ 多項式【計算】 展開や乗法公式、因数分解の公式が出てきます。因数分解は、2次方程式を解くときにも役立ちます。 ◆ 平方根【計算】 無理数(分数で表すことのできない数)へと数の世界が広がる面白い単元です。 新しい記号であるルートの計算方法を、公式として押さえておきましょう。 ◆ 2次方程式【計算】 主に3つの解き方があります。 因数分解を利用した解き方、解の公式を覚えておくと安心です。 ◆ 相似【図形】 三角形の相似条件は、合同条件との違いを意識して覚えましょう。 線分の比の関係、面積比、体積比は、入試でよく問われます。 ◆ 円【図形】 円や弧を見つけたら、円周角の定理を意識しましょう。 半円の弧に対する円周角が直角(90°)であることも覚えておくと便利です。 ◆ 三平方の定理【図形】 直角三角形の辺の長さの関係を表す定理です。 高校入試頻出で、関数もふくめ、多くの問題で応用されます。 高校入試で役立つ公式 高校入試でよく出る公式を厳選しました。 これらを重点的にマスターし、入試本番で得点アップを目指しましょう。 入試でよく出題される公式には理由があります。 それは、単に知識を問うだけでなく、複雑な問題を解く際に利用したり、他の単元にも応用できるからです。 それでは順番に見ていきましょう。 1. 三平方の定理 図形問題で辺の長さを求めるときに必須です。 平面図形だけでなく、関数や空間図形にも応用されます。 長さを求める問題が出てきたときは、三平方の定理が使えないか意識しましょう。 図形の中にひそむ直角三角形を見つけることがポイントです。 2. 2次方程式の解の公式 因数分解を利用して解けない方程式でも解ける万能な公式です。 因数分解が思いつかなくても焦らなくなります。 3. 関数とグラフの式 直線の式(1次関数の式) y=ax+b 放物線の式 y=ax2 双曲線 y= x a グラフから式や座標を求める問題は頻出です。 グラフの特長と式の形を整理しておきましょう。 比例y=axのグラフは原点を通る直線ですので、1次関数でb=0のときと覚えておくと便利です。 4. 展開・因数分解の公式 単問の計算問題だけでなく、文章題で式をつくった後の計算で利用することもあります。 2次方程式を解く際にも役立ちます。 5. 合同条件・相似条件 図形の証明問題で必須です。減点対象にもなるので、正確に書けるように覚えましょう。 辺の長さを求めるときに、図形が合同、相似であることを利用する場合もあります。 6. 円周角の定理 円に関する図形問題で、角度を求めるときによく使われます。 図形の中に円や弧を見つけたら、円周角の定理を意識して角度を調べてみましょう。 7. 多角形の内角の和・外角の和 基本的な図形問題や証明問題で使われます。 どんな多角形でも外角の和は360°ですので、外角から考えると計算しやすくなる場合もあります。 入試での使われ方と注意点 高校入試では、公式をただ覚えているだけでは点数につながりません。 公式が「どんなパターンで出題されるか」を知り、「使いこなす力」を身につけることが何よりも重要です。 例えば、三平方の定理は、関数や空間図形の中に隠れていることもあります。 公式を使えるようになるために、様々な問題を解くことが何よりも大切です。 また、一つの問題で複数の公式を組み合わせるパターンもよく出題されます。 公式を単独で覚えるだけでなく、それぞれの公式がどう連携し合っているのか、全体像を意識して学習に取り組みましょう。 「なぜそうなるか」から数学公式を理解する 公式を丸暗記するだけでは、少し問題がひねられると対応できなくなってしまいます。 公式が「なぜそうなるのか」、その成り立ちを理解することで、忘れにくく、応用も効く「使える知識」になります。 • 2次方程式の解の公式 なぜあの複雑な形になるのか? これは平方完成という考え方から導き出されます。 式の変形を順を追って理解することで、公式がより深く頭に残ります。 • 三平方の定理 なぜ a2+b2=c2 なのか? これは、直角三角形の各辺を一辺とする正方形の面積の関係を表しています。 図を使って考えることで、視覚的に理解を深められます。 • 円周角の定理 なぜ「中心角の半分になる」のか? これは補助線をひいて、二等辺三角形の性質を使うと、簡単に証明できます。 このように、「なぜ?」という疑問を持つことは、数学の面白さを発見する第一歩です。 公式を使って問題をたくさん解くとともに、その公式がなぜ成り立つのか調べてみると理解が深まります。 覚え方・使いこなし練習 公式を覚えるには、ただ眺めているだけでは不十分です。 効果的な覚え方と、実際に使いこなすための練習法を知ることが、記憶定着と応用力アップのカギとなります。 語呂合わせ・図解を活用しよう 文字ばかりの公式を覚えるのが苦手なら、語呂合わせや図解を積極的に活用しましょう。 例えば、球の表面積や体積の公式などは語呂合わせがあります。 ・球の表面積は、「心配(4π)あるある(r2)」 ・球の体積は、「身の上に心配( 4π 3 )あるから参上(r3)」 公式を覚えるときに、自分だけの語呂合わせをつくってみましょう。 友達と共有しても面白いかもしれません。 円周角の定理などは、図で視覚的に理解する方が記憶に残りやすいです。 図解が必要な公式は、自分で簡単な絵をかいたり、教科書や参考書の図をじっくり見たりして、「なぜこうなっているんだろう?」と考えてみましょう。 視覚を利用して覚えることで、いざという時に「あの図だ!」と思い出しやすくなります。 公式を使う練習のすすめ 公式は、問題演習とセットで覚えることが記憶定着のコツです。 覚えた公式を、実際に問題を解きながら使ってみることで、その使い方や、どんな時に使うべきかが自然と身につきます。 間違えた問題は、なぜ間違えたのか、どの公式の使い方が間違っていたのかをしっかり確認し、もう一度解き直しましょう。 この繰り返しが、公式を「使える力」に変える最も効果的な方法です。 おすすめの学習教材 公式の理解と定着を深めるためには、適切な教材選びも重要です。 ここで、皆さんの学習を強力にサポートしてくれる教材をご紹介します。 ◆ 中学教科書ワーク 学校の教科書の内容に沿ってつくられているため、日々の授業の予習・復習に最適です。 イラストや図解が豊富で、数学の公式も詳しく解説されています。 高校入試に有効な問題も多くふくまれており、基礎から応用まで着実に力をつけることができます。 ▶シリーズページはこちら ▶ご購入はこちら ◆ わからないをわかるにかえる ニガテなところがどんどんわかる!超基礎からやさしく学べる、中学生のための問題集! 数学の基本的な問題の解き方を丁寧に解説しています。 公式も覚えやすくなるよう配慮していますので、数学が苦手な方でも大丈夫。 小学生の先取り学習や、高校生・大人の学び直しにもおすすめです。 学年別・領域別と、高校入試シリーズがあります。 ▶シリーズページはこちら ▶ご購入はこちら ◆ 完全攻略 教科書だけではもの足りないキミに送る、定期テスト対策から高校入試の基礎固めに最適な問題集です。 ▶シリーズページはこちら ▶ご購入はこちら ◆ ハイクラス徹底問題集 最高峰の問題演習で、「試験に強い実力」をつけられる問題集です。レベルの高い問題にチャレンジしたい方に最適です。 ▶シリーズページはこちら ▶ご購入はこちら まとめ 公式を「使える力」に変えよう ここまで、中学数学の公式について、その種類から高校入試での重要性、そして効果的な学習法まで、幅広く紹介してきました。 大切なのは、公式を「知る」→「理解する」→「使えるようになる」という段階をしっかり踏むことです。 丸暗記ではなく、「なぜそうなるのか」を考え、実際に問題を解きながら使いこなす練習を続けましょう。 それが、数学の力を大きく伸ばすカギとなります。 紹介した文理の教材をうまく活用し、公式を「使える力」に変えて、自信を持って高校入試に挑んでくださいね。 皆さんの学習がより充実したものになるよう、心から応援しています!
【中学生向け】因数分解のやり方と公式一覧 テストで使えるコツも解説
もくじ はじめに 因数分解とは? 因数分解の解き方:共通因数でくくる 因数分解の解き方:4つの公式 因数分解の解き方ステップ 練習問題で確認しよう まとめと商品紹介 はじめに 今回のテーマは中学3年生の数学で出てくる「因数分解」です。 「因数分解」という言葉を聞いて、 「難しそう…」 「公式がたくさんあって覚えられない!」 と感じている人もいるかもしれません。 しかし、心配はいりません! 因数分解は、中学数学の大きな柱ですが、正しい手順といくつかのコツさえつかめば、必ず理解できるようになります! この記事では、因数分解が「なぜ大切なのか」という基礎から、テストで使える4つの公式、さらには応用問題の解き方まで、ステップごとにわかりやすく解説します。 この記事を最後まで読んで、因数分解への理解を深め、定期テストや高校入試で自信を持って問題が解けるようになりましょう! 因数分解とは? 因数分解とは、簡単に言うと「多項式をかけ算の形(因数の積の形)になおす操作」のことです。 まずは因数について確認しましょう。 例えば、6という数は、次のようにかけ算の形になおすことができますね。 6=2×3 このとき、2や3を6の因数と呼びます。 因数分解とは、多項式をいくつかの因数の積の形に分解することです。 【例】 2a2+6ab=2a(a+3b) 左側の式 2a2+6ab はたし算(単項式の和)の形ですが、 右側の式 2a(a+3b) は、2 と a と (a + 3b) という因数のかけ算の形になっています。 展開と因数分解の関係 因数分解を理解する上で、展開(てんかい)との関係を知っておくことが大切です。 因数分解は、展開の逆の操作だと考えると、イメージがしやすいでしょう。 展開:かけ算を計算して、たし算・ひき算の形になおすこと (x+2)(x+3) ― 展開 → x2+5x+6 因数分解:たし算・ひき算の形を、かけ算の形になおすこと x2+5x+6 ― 因数分解 → (x+2)(x+3) このように、展開と因数分解は、「たし算・ひき算の形」と「かけ算の形」を行き来する、裏表の関係になっています。 このイメージを持っておくと、公式を理解する際にも役立ちます。 なぜ因数分解を学ぶのか 「わざわざ式をかけ算の形になおすのはなぜ?」 と思うかもしれません。 ここでは、因数分解を学ぶ理由を3つ紹介します。 • 2次方程式を解くため x2+5x+6=0 のような2次方程式の解を求めるときは、左辺を因数分解をして、 (x+2)(x+3)=0 の形になおすことで、 x=−2 または x=−3 という解を求めることができます。 • 計算を簡単にするため 複雑な多項式を因数分解してシンプルな形にすることで、計算ミスを防ぐことにつながります。 特に、「式の値」を求めるときに役立ちます。 【例】 x=98のとき、x2+4x+4 の値を求めましょう。 直接代入して求めることもできますが、 982+4×98+4 を計算するのはたいへんです。 そこで、先に因数分解をして (x+2)2 にしてから代入します。 (98+2)2 = 1002 = 10000 と、計算が簡単になります! • 高校数学の基礎となるため 高校で学ぶより高度な数学(数Ⅱ、数Bなど)でも、因数分解は当たり前の基礎技術として使われます。 今のうちにしっかり身につけておくことが、将来の数学の土台となります。 因数分解は、定期テストでも高校入試でも必ず頻出する重要な分野です。 しっかり理解を深め、数学の基礎力を身につけましょう! 因数分解の解き方:共通因数でくくる ここからは、因数分解の解き方についてです。 因数分解をするとき、まず最初に考えるべきなのが、「共通因数でくくる」という方法です。 共通因数でくくるとは? 共通因数とは、多項式のすべての項に共通してかけられている数や文字のことです。 多項式を、共通因数と残りの部分の積の形になおす操作を、「共通因数でくくる」「共通因数でくくり出す」と言います。 これは、展開のときの分配法則の逆の操作です。 【例】 2x+6 を因数分解しましょう。 1.共通因数を見つける それぞれの項 ( 2x と 6 ) の中に共通して含まれている因数を探します。 2x=2×x 6=2×3 両方の項に共通しているのは、2 です。 つまり、共通因数は 2 です。 2.共通因数でくくる 共通因数 2 を式の前に出し、かっこでくくります。 2x+6=2(x+3) 符号と文字の扱いに注意する 多項式の最初の項がマイナスのときは、マイナスも共通因数の一部としてくくり出すことが多いです。 特に、共通因数に文字も含まれる場合は注意が必要です。 【例】 −3ab+12bを因数分解しましょう。 この式は、共通因数として数(係数)と文字の両方に着目します。 1.共通因数を見つける 数(係数)の部分 : −3 と +12 の共通因数は −3 文字の部分 : ab と b の共通因数は b です。 したがって、共通因数は −3b です。 2.共通因数でくくる −3ab+12b=−3b(a−4) 【注意】 マイナスでくくると、かっこの中の項の符号がすべて逆になることに注意しましょう。 ○ −3ab+12b=−3b(a−4) × −3ab+12b=−3b(a+4) 因数分解の解き方:4つの公式 共通因数でくくれない場合、次に因数分解の4つの公式を使います。 これらは、展開の公式を逆にしたものです。 展開の公式をしっかり覚えていると、スムーズに理解できます。 公式① x²+(a+b)x+ab=(x+a)(x+b) これは「たして (a+b)、かけて ab」になる a と b の組み合わせを見つける公式です。 【式の形】 x の項の係数が a+b(和)、定数項が ab(積)になっているのが特徴です。 【解き方のコツ】 1.まず、定数項 ab に注目し、積になる a と b のペアを考えます。 2.そのペアの中で、和が x の項の係数 (a+b) になるものを見つけます。 3.見つけた a と b を (x+a)(x+b) の形に当てはめます。 【例】 x2+7x+12 を因数分解しましょう。 1.積が 12 になるペアを探します。 (1, 12)、(2, 6)、(3, 4) … 2.その中で、和が 7 になるペアはを見つけます。 (3, 4) 3.x2+7x+12=(x+3)(x+4) 公式② x²+2ax+a²=(x+a)² 公式③ x²-2ax+a²=(x-a)² これらは、「和の平方」「差の平方」と呼ばれる公式です。 公式①で、 a=b の特殊なパターンと考えると理解しやすいでしょう。 【式の形】 xの項の係数が 2a ( a の2倍)、定数項が a2 ( a の2乗) になっているのが特徴です。 (※公式③は符号がマイナスです。) 【解き方のコツ】 1.定数項が、ある数 a の2乗になっていることを確認します。 2. x の項の係数が、1で確認したaの2倍になっているかを確認します。 3.符号に注意して (x±a)2 の形になおします。 【例】 x2−10x+25 を因数分解しましょう。 1.定数項 25 は 52 、または (−5)2 です。 2.xの項の係数 −10 は、−5 の 2 倍なので、公式③で a=5 のときだとわかります。 3.x2−10x+25=(x−5)2 公式④ x²−a²=(x+a)(x-a) (2乗)ー(2乗) の形をした因数分解の公式です。 公式①で、 b=ーa の特殊なパターンと考えると理解しやすいでしょう。 【式の形】 x の項の係数が 0 になっていて、項が2つしかないのが大きな特徴です。 【解き方のコツ】 1.式が (2乗)ー(2乗) の形になっているかを確認します。 2.(x+a)(x−a) の形に当てはめます。 【例】 x2−49 を因数分解しましょう。 1. 49 は 72 なので、x2− 72 の形です。 2.x2−49=(x+7)(x-7) 展開公式との関係 公式①から④は、すべて展開公式を逆にしたものです。 因数分解ができたら、展開し直して元の式に戻るか確認する習慣をつけましょう。 これにより、ミスが減り、公式の理解もさらに深まります。 x2+7x+12 ― 因数分解 → (x+3)(x+4) (x+3)(x+4) ― 展開 → x2+7x+12 因数分解の解き方ステップ これまでに学んだ「共通因数でくくる」方法と「4つの公式」を使えば、多項式の因数分解ができるようになります。 しかし、問題を見たときにどの方法を使えばいいか迷ってしまうことがありますよね。 ここでは、因数分解のときに迷わず正解にたどり着くためのステップを解説します。 1.共通因数を探す 因数分解を始めるとき、公式が使えるかどうかを確認する前に、必ず共通因数があるかを確認しましょう。 共通因数を見つけてくくり出すことで、その後に使う公式を見つけやすくなります。 【チェックポイント】 すべての項に共通する因数(数や文字)はないか? 【注意点】 共通因数をくくり出すのを忘れると、完全に因数分解された形にたどり着けなくなります。 2.使える公式があるか判断する 共通因数をくくりだしたあと、残った多項式を見て、どの公式が使えるかを判断します。 次のように順序だてて考えましょう。 【項が2つ】 → 公式④ x²−a²=(x+a)(x-a) が使えるか確認する 【項が3つ】 → 【定数項が a² の形になっている】 → 公式② x²+2ax+a²=(x+a)² 公式③ x²-2ax+a²=(x-a)² が使えるか確認する → 【定数項が a² の形になっていない】 → 公式① x²+(a+b)x+ab=(x+a)(x+b) が使えるか確認する 工夫して分解する応用パターン 共通因数やくくり出し、公式を組み合わせることで解ける応用問題のパターンをいくつかご紹介します。 「これ以上分解できない」状態まで分解しきるのが因数分解のゴールです。 1.複雑な式は展開してから分解する 元の式が複雑なかっこのかけ算の形になっている場合、まずは展開して同類項をまとめることで、公式が使える形になることがあります。 【例】 (x+3)(x−1)−12 ← 展開の公式を使って展開します =x²+2x−3−12 ← 同類項をまとめます =x²+2x−15 ← たして +2、かけて -15 になる数(5,-3)を探して、公式①を使います =(x+5)(x−3) 2.多項式を共通因数としてくくり出す 共通因数が数や文字ではなく、多項式になる場合もあります。 多項式全体を1つのかたまりと考えて、共通因数をくくり出します。 一見共通因数がないように見えても、一部を因数分解すると共通因数が見つかることがあります。 【例】 5(a−2)+a²−2a ← 5(a−2) と a²−2a に分けて考え、後ろの式で a をくくり出します =5(a−2)+a(a−2) ← 多項式 (a−2) が共通因数になっているので、くくり出します =(a−2)(5+a) 3.共通因数をくくり出してから公式を使う 共通因数でくくり出したあと、さらに因数分解できる場合があります。 因数分解できるかどうか、必ず最後までチェックしましょう。 【例】 3x³y−12xy³ ← 共通因数 3xy でくくり出します =3xy(x²−4y²) ← x²−4y² で、公式④を使って因数分解します =3xy(x+2y)(x-2y) 4.x² の項の係数が1でない式 x² の項の係数が常に1とは限りません。 そんな式でも、公式②または③が使える場合があります。 何かの2乗になっているか考えるのがポイントです。 【例】 9x²−6xy+y² ← 公式が使える形に変形します =(3x)²−2×3x×y+y² ← 公式③を使います =(3x−y)² 練習問題で確認しよう これまでの知識が定着しているか、以下の問題で確認してみましょう。 因数分解は、「共通因数」→「公式」の順番で考えることが大切です! 【問題】 次の式を因数分解しましょう。 1.4x²−16x 2.a²+8a+15 3.25x²−16y² 4.3x²−30x+75 5.(x+3)²−5(x+3) 【ヒント】 解き方に迷ったら、以下のヒントを参考にしてください。 1.まずは、数と文字の共通因数を見つけて、くくり出しましょう。 2.公式①のパターンです。たして +8、かけて +15 になる2つの数を探しましょう。 3.(2乗)ー(2乗) の形です。公式④を使いましょう。 4.最初に共通因数の3をくくり出し、かっこの中の式で公式③を使います。 5. (x+3) を共通因数としてくくり出しましょう。 【解答と解説】 1. 4x²−16x ← 共通因数 4x でくくり出します =4x(x−4) 2. a²+8a+15 ← たして 8 、かけて 15 になる組 (3,5) を見つけます =(a+3)(a+5) 3. 25x²−16y² ←(2乗)ー(2乗) の形にします =(5x)²ー(4y)² ← 公式④を使います =(5x+4y)(5x-4y) 4. 3x²−30x+75 ←共通因数 3 をくくり出します =3(x²−10x + 25) ← かっこの中で、公式③を使って因数分解します =3(x−5)² 5. (x+3)²−5(x+3) ←共通因数 (x+3) をくくり出します =(x+3){(x+3) - 5} ← かっこの中を整理します =(x+3)(x - 2) まとめと商品紹介 いかがでしたか。因数分解の基本を理解したら、あとは定着させるために練習あるのみです。 因数分解の知識を確かな力に変えるために、あなたのレベルに合った文理の教材で次のステップに進みましょう! おすすめの商品 因数分解の基本と応用を理解したら、あとは練習あるのみです。 文理では、お客様ひとりひとりのレベルや目的に合わせた教材をご用意しています。 ここでは、あなたの学習を次のステップに進めるための、おすすめの商品を3シリーズご紹介します。 わからないをわかるにかえる ▶シリーズページはこちら ▶ご購入はこちら 因数分解を基礎からじっくり学びたい、これまでどこから手をつけていいかわからなかったという人に最適なシリーズです。 この教材は、「わからない」を「わかる」にかえることを徹底的に追求しています。 定義や公式といった基礎的な内容を、簡単な例題で丁寧に解説しているため、因数分解が苦手な人でも、着実に基礎から練習を積み重ねることができます。 簡単なステップで自信をつけながら学習を進めたい方に、特におすすめします。 完全攻略 ▶シリーズページはこちら ▶ご購入はこちら 因数分解の知識を深め、確かな実力をつけたいなら「完全攻略」シリーズが役立ちます。 このシリーズは豊富な演習量が特徴で、基礎の反復から応用までしっかりと問題演習をこなすことで、因数分解を完全に理解し、定着させることができます。 また、定期テスト対策ページや、過去の入試問題を扱った実戦問題ページも収録されているため、日々の学習から受験対策まで幅広い学習に対応可能です。 学校の授業の進度に合わせて使いたい方にも最適です。 ハイクラス徹底問題集 ▶シリーズページはこちら ▶ご購入はこちら 難易度の高い問題に挑戦し、数学の応用力を圧倒的につけたい人向けの最高峰の問題演習集です。 この問題集では、因数分解の複雑な応用問題や、複数の知識を組み合わせる思考力を要する問題を豊富に扱っています。 難関高校の入試問題も収録されているため、ハイレベルな演習を通じて、ライバルに差をつけたいと考えている学習者を徹底的にサポートします。 現在の学習レベルに関わらず、数学を極めたいという意欲のある方は、ぜひ手に取ってみてください。