アゲモノ【第1回】「三平方の定理」

学び直したい大人に贈る連載「アゲモノ」
昔習った気がするあれやこれ…
少し思い出してみませんか?
おいしいアゲモノが一緒だから、サクサク取り組めます
問題
スーパーマーケットで揚げ物を選んでいるとき、トングとアジフライの間に直角三角形が見えることが気になってきた。
次の三角形ABCについて、辺BCの長さを求めなさい。
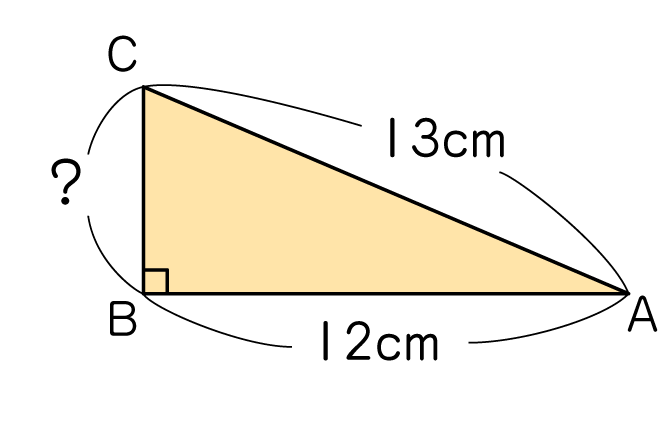
※この下へスクロールするとヒント①が見えますのでご注意ください。
ヒント①
三平方の定理を使ってみよう。
三平方の定理ってなんだっけ?となったらヒント2へ
※この下へスクロールするとヒント②が見えますのでご注意ください。
ヒント②
三平方の定理は
直角三角形において、斜辺(直角と向かい合う辺)以外の2つの辺の長さをそれぞれ2乗して足すと、斜辺の長さの2乗と等しくなる、
という公式。
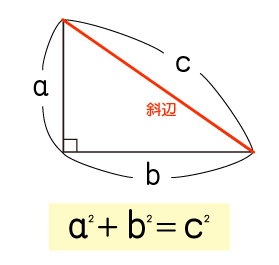
ちなみに、2乗とはその数を2回かけ算すること。
2の2乗=2×2=4
2の3乗=2×2×2=8
※この下へスクロールすると解答が見えますのでご注意ください。
解答・解説
解答 5cm
三平方の定理によると、
直角三角形において、a²+b²=c² が成り立つ。

問いの直角三角形ABCについて
a=BC、b=AB、c=CAとして、三平方の定理を使うことができる。
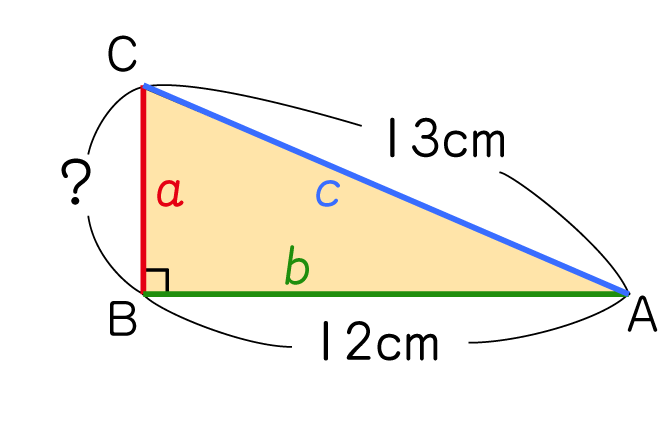
a²+b²=c²
⇒ BC²+AB²=CA²
AB=12、CA=13なので、
BC²+12²=13²
これを計算していくと、
BC²=13²-12²
BC²=169-144
BC²=25
BCは2乗して25になる数字なので、5または-5があてはまるが、三角形の辺の長さが負の数や0になることはありえない(BC>0)
よって、BC=5
次回もお楽しみに!

学び直しおすすめ書籍
①大人の教科書ワーク


ちょっとしたギモンを小中学校の教科書を振り返りながら解説!
「なにかやってみたい」「読み物として楽しみたい」
そんなあなたにおすすめ。

▲日常の悩みやギモンを、小中学校の教科書で解決!
②わからないをわかるにかえる学年別・領域別


中学生向けの超基礎シリーズ。
中学校の学習に沿ってやり直したい人におすすめ。
平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。
 ▲基礎をいちからていねいに学び直したいときに
▲基礎をいちからていねいに学び直したいときに
③コーチと入試対策!3年間の総仕上げ


短期間で高校入試対策シリーズ。
要点だけ、さらっとやり直ししてみたい人におすすめ。
1教科10日間で中学3年間をざっと確認できます。

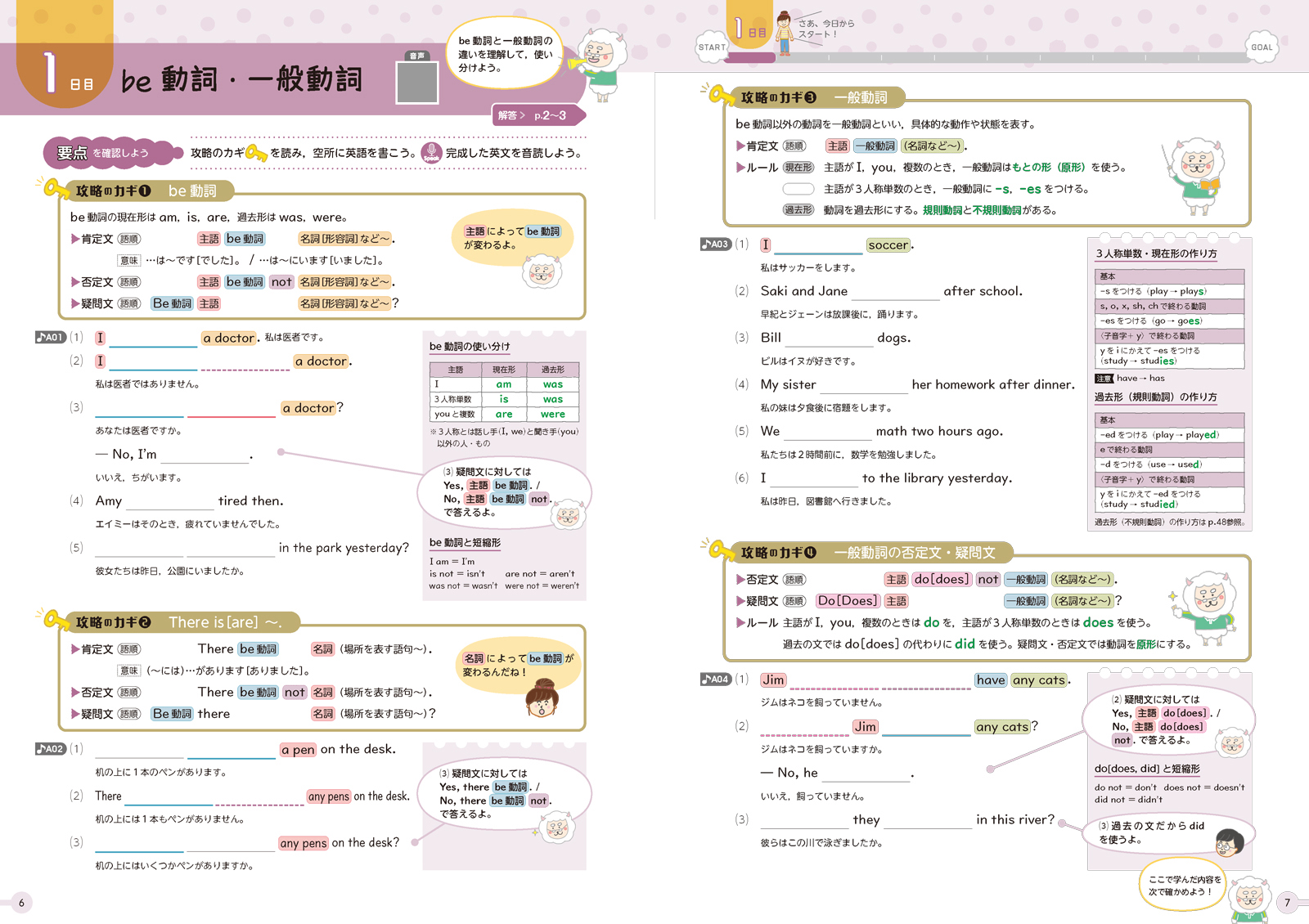
▲紙面もかわいく、キャラクターによるヒントが豊富です
関連記事
アゲモノ【第2回】「月の見え方」
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 問題 運ばれてきたとんかつの付け合わせのレモンを見て、ちょっと気の利いた事を言いたくなった。次のセリフの( )に当てはまる言葉として、正しいものを選びなさい。 このレモン、( 上弦の月 /下弦の月 )が沈んでいくところみたいだね ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① とんかつを地平線に見立ててみよう 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② 上弦・下弦の由来は諸説あるが、半月を弓に見立てたとする説がある。 弓の、弦(つる)とよばれる部分はここ。 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 解答 上弦の月 月を弓に見立てたときに、月が沈む時間に弓の弦(つる)の部分が上に来ているのが上弦の月。半月を見つけたら、言ってみよう! 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら
アゲモノ【第3回】「野菜の切り方」
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 問題 揚げ物ばかりじゃなく野菜も食べよう!次の野菜の切り方の名前として、それぞれ正しいものをあとのア~オから選びなさい。 ア いちょう切りイ くし形切りウ ささがきエ 半月切りオ 小口切り ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① ささがきは、「笹掻き」と書く。笹の葉はどんな形? 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② くし形切りはトマトや玉ねぎ、リンゴなど球体のもので使われる切り方 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 ①エ ②ア ③オ ④ウ いちょう切り・くし形切り・半月切りは、それぞれ切った時の形がいちょう・櫛・半月ににているためにその名がついた。ささがきも、「笹掻き」と書き、切った時の形が笹の葉に似ていることから。小口切りの小口は「材料の端」を指し、端から切っていくのでこの名がついた。 ちなみに、「小口」というのは印刷用語でも登場する。本の外側を「小口」・内側の綴じる方を「のど」とよぶ。 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら
アゲモノ【第4回】江戸時代の改革
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 問題 日本で天ぷらが広まったのは江戸時代ですが、江戸時代の幕府の政治について、次のア~エを起こった順に並べなさい。 ア 水野忠邦が天保の改革を行った イ 徳川吉宗が享保の改革を行った ウ 松平定信が寛政の改革を行った エ 田沼意次による政治が行われた ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① 松平定信は徳川吉宗を手本とした。水野忠邦は、田沼意次が奨励した株仲間を解散させた 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② 寛政の改革は非常に厳しかったため、次のような狂歌が読まれた「白河の清きに魚も棲みかねて もとの濁りの田沼恋しき」 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 イ→エ→ウ→ア 享保の改革:1716~1745年田沼意次の政治:1772~1786年寛政の改革:1787~1793年天保の改革:1841~1843年 享保の改革・寛政の改革・天保の改革は合わせて三大改革とよばれる。いずれも、幕府の財政を立て直すために行われた。三大改革はいずれも質素倹約を奨励し、田沼意次は商業を奨励した。 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら
アゲモノ【第5回】「文節のはたらき」
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 問題 次の下線部で示した文節のはたらきとして正しいものを、あとのア~オからそれぞれ選びなさい。 ぼくはその日、①サックサクのコロッケを買った。 早く帰ろうと、②いそいそと歩き出したが、ついにがまんできず、一口ほおばってしまった。 その瞬間、なんともいえない幸せな気持ちが胸に③広がった。 ア 主語イ 述語ウ 連体修飾語エ 連用修飾語オ 接続語 ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① 修飾語は、「何を」「いつ」「どこで」「どのように」など、他の文節の内容を説明する働きをもつ。連体修飾語は体言を、連用修飾語は用言を詳しく説明するもの。 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② 体言は名詞のこと。用言は動詞や形容詞、形容動詞のこと。 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 ①ウ ②エ ③イ ぼくはその日、①サックサクのコロッケを買った。 ①=ウ 連体修飾語 早く帰ろうと、②いそいそと歩き出したが、ついにがまんできず、一口ほおばってしまった。 ②=エ 連用修飾語 その瞬間、なんともいえない幸せな気持ちが胸に③広がった。 ③=イ 述語 ①は、「コロッケ」の状態を説明しています。「コロッケ」は体言(名詞)なので、連体修飾語です。 ②は、「歩き出した」の様子を説明しています。「歩き出した」は動詞、つまり用言なので、連用修飾語です。 ③は、主語「気持ちが」に対応した述語です。 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら
アゲモノ【第6回】「円の面積」
学び直したい大人に贈る連載「アゲモノ」 昔習った気がするあれやこれ… 少し思い出してみませんか? おいしいアゲモノが一緒だから、サクサク取り組めます 質問 この図形は何に見えますか? ▼選択してください▼ エビフライ トンカツ からあげ 本当にそうでしょうか? 戻る▲ そう!エビフライに見えますね。 では問題 このエビフライのように見える図形の面積を求めなさい。円周率はπとする。 ヒントを見る▼ 解答・解説へ▼ ※この下へスクロールするとヒント①が見えますのでご注意ください。 ヒント① 半径rの円の面積は、πr² また、半径r、中心角a°のおうぎ形の面積は、πr²×a/360 問題にもどる▲ ヒント②へ ▼ 解答・解説へ▼ ※この下へスクロールするとヒント②が見えますのでご注意ください。 ヒント② パズルのようにぴったりはめると…?しっぽの部分を足すのも忘れずに。 問題にもどる▲ ヒント①へ ▲ 解答・解説へ▼ ※この下へスクロールすると解答が見えますのでご注意ください。 解答・解説 解答 36πcm² 小さい半円を図のように移動させると、 衣の部分を大きな円の半分と見なすことができます。 この大きな円の半径は8cmなので、衣の面積は、π×8²×1/2=32π(cm²)です。 しっぽの部分を忘れずに足します。この部分は、半径4cmの円の1/4なので、面積は、π×4²×1/4=4π(cm²)となります。 求める面積は、32π+4π=36πより、36πcm² です。 ★ちなみに★ πは「周囲(perimeter)」の意味を持つギリシャ語 περίμετρος (ペリメトロス) の頭文字です。 問題にもどる▲ 次回もお楽しみに! 学び直しおすすめ書籍 ①大人の教科書ワーク ちょっとしたギモンを小中学校の教科書を振り返りながら解説! 「なにかやってみたい」「読み物として楽しみたい」 そんなあなたにおすすめ。 ▲日常の悩みやギモンを、小中学校の教科書で解決! ▶シリーズページはこちら ▶ご購入はこちら ②わからないをわかるにかえる学年別・領域別 中学生向けの超基礎シリーズ。 中学校の学習に沿ってやり直したい人におすすめ。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▲基礎をいちからていねいに学び直したいときに ▶シリーズページはこちら ▶ご購入はこちら ③コーチと入試対策!3年間の総仕上げ 短期間で高校入試対策シリーズ。 要点だけ、さらっとやり直ししてみたい人におすすめ。 1教科10日間で中学3年間をざっと確認できます。 ▲紙面もかわいく、キャラクターによるヒントが豊富です ▶シリーズページはこちら ▶ご購入はこちら ④旅するワーク 「地球の歩き方」とコラボした新シリーズ! 世界の国々の地理・歴史について、旅行気分で学び直してみませんか? 「知らなかった!」となる豆知識もたっぷりで、大人でも楽しめます! ▲地球の歩き方ライターによるコラムも豊富で読み応え抜群! ▶シリーズページはこちら ▶ご購入はこちら




