2025/05/14
小学生でもわかる！パーセント計算のやり方とコツ
はじめに
「この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は…」
「水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何％かな？」
「この服、4500円だけど30%オフになっているよ！いくらになるのかな？」
私たちの生活の中には、パーセント(%)という言葉がたくさん出てきます。
パーセントを理解すると、身の回りのことがよくわかるようになります。
この記事では、小学生のみなさんにもわかりやすいように、パーセントの基本的な考え方、計算方法、ちょっとしたコツなどを紹介します。
パーセントの世界を一緒に探検してみましょう！
パーセントの計算ができる文理のドリルシリーズはこちら！
パーセントとは？
◆パーセントの意味
普段の生活の中でパーセント(%)という記号をよく見かけますよね。
これは、
「全体を100としたときにどのくらいあるか」
を表す記号です。
「％」を使って表す割合を、百分率といいます。
全体を100(百)としているので百分率です。
たとえば、全体で100人いる中で、20人がめがねをかけているとき、めがねをかけている人は「20%」になります。
全体を100として考えることで、全体の数が半端な数であっても、どのくらいあるかわかりやすくなります。
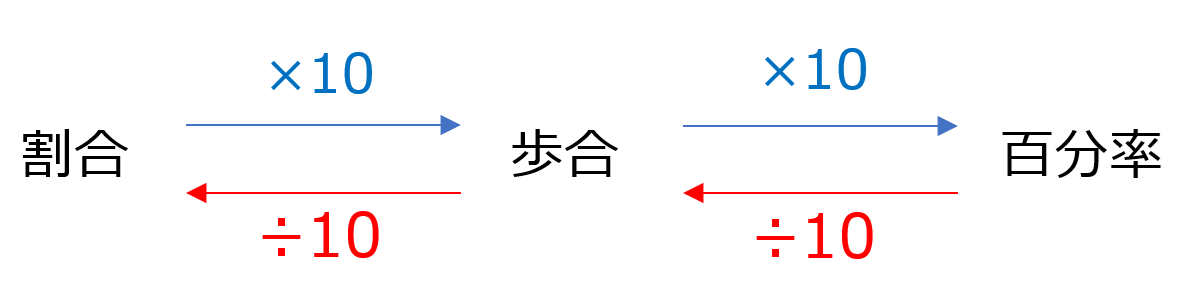
◆割合、歩合、百分率の関係
百分率と合わせて、割合や歩合という言葉も使われます。
これは、全体を何にするかで使い分けます。
・割合 → 全体を1としたときにどのくらいあるか。
単位はつけません。
・歩合 → 全体を10としたときにどのくらいあるか。
単位は割(わり)、分(ぶ)、厘(りん)などを使います。
・百分率 → 全体を100としたときにどのくらいあるか。
単位は％です。
割合を10倍すると歩合、割合を100倍すると百分率になります。
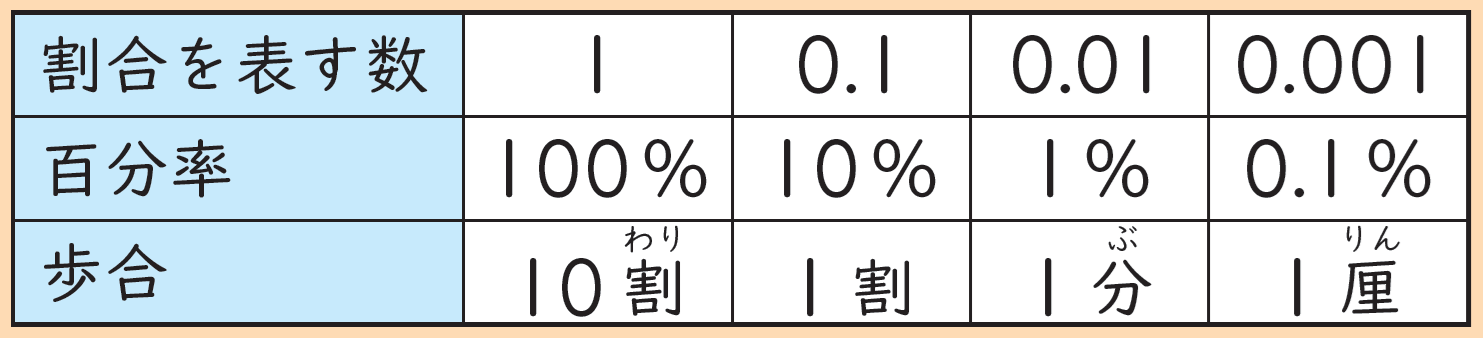
具体例で確認してみましょう。
全体で100人いる中で、20人がめがねをかけているとき、
・割合 → 0.2 (20÷100=0.2)
・歩合 → 2割 (20÷100×10=2)
・百分率 → 20% (20÷100×100=20)
となります。
３つの関係を表にまとめると、関係がわかりやすくなります。
歩合が使われることは減っていますが、野球の打率を表すときに使われます。
例：文理野球部４番バッターの今年の打率は、3割ちょうどでした。
この場合、このバッターは、10打席中３打席ヒットやホームランを打つと考えられます。
パーセント計算の基本ルール
◆「○○の□□％」を計算する方法
ここからは、テストでもよく出る問題の解き方を、パターン別に解説します。
解き方を確認したら、練習問題にもチャレンジしてみましょう！
例題
400円の20％は？
解き方・答え
計算するときは、百分率を割合に直します。
20% → 0.2 (20÷100=0.2)
400×0.2＝80(円)
20のまま計算しないよう注意しましょう。
では、練習問題です！
練習問題
★次の計算をしましょう。
１．800gの20％は？
２．600Lの30％は？
３．700人の15％は？
４．この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は…
↑４は、はじめにで紹介した問題です！
解き方・答え
１．20% → 0.2
800×0.2=160(g)
２．30% → 0.3
600×0.3=180(L)
３．15% → 0.15
700×0.15=105(人)
４．10% → 0.1
500×0.1=50(ｍL)
パーセントを使って計算するときは、百分率を割合に直すことを忘れないようにしましょう。
◆「□□は○○の何％？」を計算する方法
次は、割合を計算してからパーセントを求める問題です。
例題
80円は400円の何％？
解き方・答え
まず、割合を求めます。
80÷400=0.2
何％か求めるので、100をかけて百分率に直しましょう。
0.2×100=20(%)
では、練習してみましょう！
練習問題
★次の計算をしましょう。
１．50gは200gの何％？
２．48Lは80Lの何％？
３．150人は1250人の何％？
４．水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何％かな？
解き方・答え
１．50÷200=0.25
0.25×100=25(%)
２．48÷80=0.6
0.6×100=60(%)
３．150÷1250=0.12
0.12×100=12(%)
４．6÷300=0.02
0.02×100=2(%)
百分率(パーセント)で答えるので、100をかけて百分率に直すことに注意しましょう。
割引や増加・減少とパーセント計算
◆割引とパーセント
お店で買い物をするときに、「30%オフ！」というPOPを見かけることはありませんか？
これは、元の値段から30%安くなることを表しています。
割引されるときのパーセントの計算を確認しましょう！
例題
5000円の服が40%オフで売られています。支払う金額はいくらですか？
解き方・答え
40%が0.4であることに注意して、まずは安くなる金額を求めます。
5000×0.4=2000(円)
次に、支払う金額を求めます。
5000-2000=3000(円)
では、練習してみましょう。
練習問題
★次の問題に答えましょう。
１．800円のお菓子が15%オフで売られています。支払う金額はいくらですか？
２．2500円の商品が20%オフになっています。支払う金額はいくらですか？
３．定価12000円の自転車が35%オフで売られています。支払う金額はいくらですか？
４．この服、4500円だけど30%オフになっているよ！いくらになるのかな？
解き方・答え
１．800×0.15=120(円)
800-120=680(円)
２．2500×0.2=500(円)
2500-500=2000(円)
３．12000×0.35=4200(円)
12000-4200=7800(円)
４．4500×0.3=1350(円)
4500-1350=3150(円)
◆増える・減るときのパーセント
増えたり減ったりするときにもパーセントは使われます。
例題
タケルさんの今回のテストの点数は、前のテストの点の80点より15%増えました。
今回のテストは何点でしたか？
解き方・答え
まず、増えた点数を求めます。
80×0.15=12(点)
次に、今回の点数を求めます。
80+12=92(点)
では、練習問題です！
練習問題
★次の問題に答えましょう。
１．ユイさんの身長は、１年前に150cmでしたが、この1年で5%伸びました。今の身長は何cmですか？
２．A地域の人口は、昨年10000人でしたが、今年は2%減りました。A地域の今年の人口は何人ですか？
３．お父さんの体重は60kgでしたが、ダイエットをして10%減らしました。ダイエット後の体重は何kgですか？
解き方・答え
１．150×0.05=7.5(cm)
150+7.5=157.5(cm)
２．10000×0.02=200(人)
10000-200=9800(人)
３．60×0.1=6(kg)
60-6=54(kg)
より多くの問題を解きたい方はこちら！
パーセントの計算をもっと楽しくするコツ
◆暗算のちょっとしたテクニック
ここからは、知っていると便利なテクニックを紹介します。
よく出るパーセントの計算方法を覚えておくと、暗算で答えが出せるようになることがあります。
・10% → 元の数を10でわるのと同じ！
例：290円の10%は？
290÷10=29(円)
・50% → 元の数を2でわるのと同じ！ (元の数の半分！)
例：800個の50%は？
800÷2=400(個)
・25% → 元の数を4でわるのと同じ！ (元の数の4分の1！)
例：200ページの25%は？
200÷4=50(ページ)
・20% → 元の数を5でわるのと同じ！
例：500mLの20%は？
500÷5=100(mL)
これらのテクニックを覚えておくと、暗算できることがあります。
◆クイズでパーセントをマスターしよう！
ここまで学習してきたパーセントの計算を使って、クイズに答えてみましょう。
問題
★次の問題に答えましょう。
１．定価1000円のものが60%オフで売られています。
財布に500円しかないとき、この商品を買える？買えない？
２．50点満点のテストの結果が40点でした。90%正解したことになる？
３．果汁20%の飲み物を２本買って混ぜたら、果汁は40%になる？
４．450円の80％と、700円の50％では、どちらが安い？
解き方・答え
１．1000×0.6=600(円)
1000-600=400(円)
500円あるので買えます。
答え 買える。
２．40÷50=0.8
0.8 → 80%
答え 90%正解したことにはならない。
３．果汁20%の飲み物を何本混ぜても、果汁は20%のままです。
答え 果汁40%にはならない。
４．450×0.8=360(円)
700×0.5=350(円)
答え 700円の50％の方が安い。
計算が得意になる！ おすすめ問題集
文理の書籍には、計算練習ができるものがたくさんありますので紹介します。
今回紹介したパーセントの計算以外の計算問題もたくさんあります。
計算力をつけるには問題をたくさん解くことが一番！
力をつけたい方はぜひチャレンジしてみてください。
※パーセントの問題は、小学5年生で詳しく学習します。
パーセントの問題を練習したい方は、小学５年生の書籍をご利用ください。
◆小学教科書ワーク 「算数」
教科書に完全対応しているから、学校の授業に合わせて使いやすい！
計算練習ノート、ポスター、動画、CBTなど付属品も充実！
全教科書に対応した「数と計算」「文章題・図形」シリーズも用意しています。
◆小学教科書ドリル 「算数」
1回10分で終わるドリルだから、習い事など忙しくても続けやすい！
基本・確認の２ステップで、無理なく力がつきます！
計算問題に特化した「計算編」文章題や図形問題に特化した「文章題、数・量・図形」シリーズも用意しています。
◆できる!!ふえる↑ドリル
１枚ずつはがして使えるから、学習しやすい！
「計算」「文章題」「数・量・図形」「時こくと時間」など、分野別のシリーズが充実しています。
◆ハイレベル算数ドリル
3段階構成で取り組みやすい！
詳しい回答解説で、学習をサポート！
まとめ
今回の記事では、パーセントの基本的な意味から、計算の仕方、そしてちょっとしたコツまでを解説してきました。
パーセントは、私たちの身の回りの色々なところで使われています。
色々な問題にチャレンジして、パーセントマスターを目指してくださいね！
関連記事
小学生におすすめの「自主学習ネタ」まとめて紹介
「自主学習」は、まさに文字通り、自分が主体的に学習することです。 家庭での学習というと、「宿題をやる」がありますが、これは学校の先生から与えたれたもので、他人からのものです。 宿題は与えられた課題を指示のとおりにこなすことで、自主学習とは違います。 自分で内容や順序などを考え、自分の方法で学習していくことが自主学習といえるでしょう。 ここでは、自分で学ぶことの意義や重要性をわかりやすく解説していければと思います。 もくじ 小学生にとって自主学習が重要な理由 自主学習ネタの選び方 保護者におすすめ！小学生向け科目別の自主学習ネタ 家庭で自主学習を効果的にサポートする方法 親子で一緒に学ぶ楽しさ まとめ 小学生にとって自主学習が重要な理由 自分の経験からしても、宿題はやらないといけない、やらされている感が強く、どうしても後ろ向きなイメージです。楽しくはないものの認識です。 一方、自主学習は、子どもが自分で考えて進めるので、宿題のようにやらされている感じはなく、その点だけでも取り組む姿勢が違ってきます。 取り組む姿勢が違ってくると子どもは学ぶことが楽しいことと思えてきます。 自分で考え、学習することで、意欲を引き出し、前向きに取り組めるようになります。 勉強だけでなく、何事にも前向きに取り組むようになる、そんなきっかけになるかもしれません。 自分で考える力が育つ 自主学習をするようになると、自主的に課題を見つけることもありますし、それを解決することによって、論理的思考が育まれます。順序立てて考える力がつき、将来に起こるかもしれない様々な問題を解決する力もつくでしょう。勉強においては、学習の自主性に間違いなく役に立ちます。 小学生で密につけば、中学、高校の学習スタイルの土台にもなりえるでしょう。 興味を深めることができる どうしても勉強は与えらえてやるものという印象でした。これが、自主学習で自分の好きなことや興味のある分野を深堀りすることで学びの楽しさを体感できます。 そうして、学ぶことは楽しい！となると、さらに学ぼう！と学ぶ意欲が高まっていくのです。 自信がつく 自分で自主的に取り組んだ結果、できた！これもできた！ こっちもできた！と成功体験を得ていくことで自信がつきます。 そうすると、さらに学習意欲が増します。好循環です。 そのような姿を見られるようになり、保護者の方も子どもの成長を感じられるようになるので、このような体験の積み重ねがとても大切です。 自主学習ネタの選び方 それでは自学自習のテーマ（ネタ）はどんなのがあるのでしょう。子どもに合った自学自習のテーマの選び方の例を見ていきたいと思います。 好きな科目や得意なことを軸にする 自学自習するテーマを何がいいか、迷いますよね。 世の中には様々な事象がありますから。 とはいえ、難しく考えることはありません。まずは、子どもの得意な教科をもとにテーマを選ぶのがいいでしょう。社会が得意なお子さんでしたら社会を基にすればいいですし、国語でも、算数、理科でも、それぞれのお子さんに合った教科を基にテーマを選べば、子ども自身が興味を持って取り組みやすくなります。 日常の興味を学びに変える 必ずしも学校の教科から始めないといけないわけではありません。普段の遊びや興味からスタートでもいいのです。 たとえば、虫取りが好きなお子さんがいたら、とんぼの観察から始めて、そこからとんぼの体のつくりを調べたり、とんぼのなかまは何だろうと、興味のあるところから、学びにつなげていければいいのです。 絵を描くことや料理でも構いません。 学校の勉強に沿ったテーマを選ぶ 学校の教科からテーマを選ぶのもいいといいましたが、そこをもう一歩進めて、教科の学習内容に関連するのもいいでしょう。その方が、授業の予習・復習に直結し、直接的に役に立ちますので、学校の勉強がより理解しやすくなります。 参考書を使う 基本的なやり方ですが、お持ちの問題集や参考書を使ってやる方法もあります。 ご自宅にある問題集でもいいですし、お子さんが興味を示した参考書を書店で買って、自主学習をするのもとてもいいです。 問題集や参考書には、それぞれ特徴があり、それらの後押しもあって、自主学習の質が向上する一助となることもあるでしょう。 保護者におすすめ！小学生向け科目別の自主学習ネタ ここでは保護者の方が、お子さんと一緒に取り組めるネタ、そして、子どもが自発的に取り組みやすいネタを科目別に紹介していこうと思います。 国語の自主学習ネタ 低学年 例①かんたんなお話作り ②ひらがなやカタカナの練習 ③お絵かき日記 ④好きな絵本の音読 など 中学年 例①物語作り ②短い日記 ③簡単な読書感想文 ④漢字の書き取りやかるたで遊ぶ ⑤漢字の成り立ち など 高学年 例①長めのお話作り ②詳細な読書感想文 ③新聞記事の要約 ④難しい漢字の使い方や四字熟語の練習 など 算数の自主学習ネタ 低学年 例①お金の計算ごっこ ②数の数え方や足し算・引き算のゲーム ③かんたんな形のパズル など 中学年 例①掛け算九九チャレンジ ②長さや重さの測定 ③三角形や四角形などの図形パズル など 高学年 例①分数や小数の計算練習 ②算数のトリック問題 ③図形の面積や体積を求める問題 ④速さや割合の計算 など 理科の自主学習ネタ 低学年 例①花や木の観察日記 ②身近な生き物や昆虫の観察 ③日光や風の体験実験（水に色をつけて蒸発させるなど） など 中学年 例①植物の成長観察（豆の栽培など） ②簡単な家庭実験（食塩水の結晶づくり） ③天気予報の観察と記録 など 高学年 例①複雑な家庭実験（酸・アルカリの反応など） ②気象観測（気温・湿度の記録） ③地域に生息する生き物の調査 など 社会の自主学習ネタ 低学年 例①地域の名所や神社・公園を訪れて観察 ②家族の職業や役割について話し合う ③おうちの近くの地図作り など 中学年 例①地域の行事や祭りについて調べる ②家族の歴史（祖父母の話を聞くなど） ③簡単な都道府県カードゲームで日本地図を学ぶ など 高学年 例①町や市の歴史調べ ②戦国武将や歴史上の人物について調べる ③47都道府県の特産品や名所を覚えるゲーム など 自由研究の自主学習ネタ 低学年 例①かんたんな工作（折り紙で動物を作るなど） ②好きな動物の絵を描く ③身近な植物や昆虫の観察記録 など 中学年 例①少し複雑な工作（ペットボトルの船など） ②家でできる簡単な実験（重曹とお酢で泡を作るなど） ③動物や魚について詳しく調べる など 高学年 例①科学実験（電池で動く工作など） ②音楽や絵画の鑑賞記録・感想文 ③複雑な動植物の生態や自然環境についての研究 など 家庭で自主学習を効果的にサポートする方法 それでは、保護者が子どもの自主学習をサポートする際の具体的な方法について、紹介していきたいと思います。 1日少しずつ学ぶ習慣をつける 大人でも言えますが、何事も少しずつで、習慣づけることが大切です。 毎日、少しの時間でも続けていき、続けることの大切さを教えていきましょう。 例えば、友達と遊びに行く前にドリルをやる、とか、ゲームをやったら、そのあとは１０分漢字練習をする、とか、どんなことでも短くてもいいので、学ぶ習慣をつけていきましょう。 目標とごほうびを設定する やみくもに「やれ！」ではやりません。 小さなことからコツコツと、で、まず小さな目標を設定し、それを達成していく。達成したらお子さんは喜びます。喜びを積み重ねることが一番の近道です。 そして、達成したらごほうびを、というか、何か報酬的なものあげることもいいです。 ワークを３０分したら、ゲームしていいよ、でもいいですし、しっかりほめてあげることも大切です。 結果よりプロセスをほめる 例えば自学自習でやったテストで100点取った結果をほめるのもいいですが、結果だけでなく、その過程での努力もほめてあげましょう。 まとめのテストでいい点とれたけど、それよりもまして、そこまでの毎日の問題演習を頑張ったね！とか、途中で間違えた問題も戻って解きなおして、できるようになったね！など、 ほめて、子どもの自信を育むことも重要です。 親子で一緒に学ぶ楽しさ 特に低学年のお子さんはそうですが、なかなか毎日机に向かうということも難しいかもしれません。 ただ、保護者の方が一緒に横に座って最初はやってみると、お子さんもやり始めやすいでしょうし、親子の絆も深まります。 お子さんも自主学習をしていて、疑問に思うこともあるでしょう。あれ、どうして？ なぜ？ と質問してきたときに近くにいてあげて、一緒に学ぶと子どもたちは喜んでやってくれるかもしれません。 まとめ 「自主学習」は自分が主体的に学ぶことです。 自主学習をするようになると、考えますので、成長します。 始めるには、まずはスモールステップをクリアし、少しづつ進めていくことです。 それらの家庭での学びを保護者はサポートすることで、子どもの成長をそ促進できることになります。 そのためには・・・と意気込むより、 「まずは一つ、自主学習ネタを子どもと一緒に考えてみましょう！」 自主学習におすすめ 文理の「ふしぎはっけん！ たんきゅうブック」 親子で一緒に身の回りのふしぎを探求し、完成させる体験学習ブック！ 好奇心・探求心をのばすためのファーストブック ♪ ▶シリーズページはこちら ▶ご購入はこちら 【今回の執筆者】 イニシャル：KN 年代：50代 ～今回の一言～ 一歩、また一歩、足音を踏み鳴らそう♪
素数とは？中学数学で押さえておきたいポイント
もくじ 素数って何？基本を知ろう 素数は中学数学でどのように使うの？ 素数を見分ける方法 素数に関するよくある質問 素数の面白い応用例 「わからないをわかるにかえる数学」 「大人の教科書ワーク 数学」 まとめ 素数って何？基本を知ろう 素数の定義をわかりやすく 素数とは、「１とその数自身の積でしか表せない自然数のこと」です。 言い換えると、「１とその数以外に約数ををもたない（約数が２つの）自然数」が素数となります。 ２、３、５、７、・・・ などが素数ですが、例えば７は、１と７でしか割り切れませんから、素数です。 ４や６は、１とその数自身でも割り切れますし、それぞれ２と３でも割り切れますので、素数ではありません。 素数を中学数学で学ぶ理由 素数は、数学の基礎となり、中学数学・高校数学を学ぶうえで必要不可欠な知識となります。 中学では、素数は「素因数分解」や「平方根」で使います。 自然数を素数の積だけで表す素因数分解では、言うまでもなく素数が重要な役割をもっています。 また、小学校５年生で習う「最大公約数・最小公倍数」でも、実は素数が鍵となっています。 数学の基礎となる素数はしっかりと理解を深めておく必要があります。 素数は中学数学でどのように使うの？ 素因数分解で使う例 自然数を素数の積だけで表すことを素因数分解といいます。 素因数分解の基本手順はしたのようになります。 したがって、８４を素因数分解すると、２×２×３×７となります。（実際の問題に答える際には、２²×３×７としましょう。） 最大公約数・最小公倍数の計算での役割 先ほど、最大公約数・最小公倍数で素因数分解が使えると書きましたが、どのように使うのでしょうか。 たとえば、９０と１６２の最大公約数と最小公倍数を考えます。 ９０と１６２をそれぞれ素因数分解すると、こうなります。 これを、下のように縦にそろえて書きます。 ９０と１６２の最大公約数は、したのように考えて、１８だということがわかります。 ９０と１６２の最小公倍数は、したのように考えて、８１０だということがわかります。 このように、最大公約数や最小公倍数を求める際には、素因数分解が役立ちます。 素数を見分ける方法 小さな数で割り算してみる 素数かどうかを見分けるために、小さな数で割り算をしてみるという方法があります。 【手順】 １. まず２で割ってみる 偶数はすべて２で割り切れるので、２以外の偶数は素数ではありません。 例：４、６、８…は２で割り切れるので素数ではない。 ２. 次に３で割る ３で割り切れる場合、その数も素数ではありません。 例：９、１２、１５…は３で割り切れるので素数ではない。 ３. ５で割る 最後の数字が０か５で終わる数は、５で割り切れるため、素数ではありません。 例：１０、１５、２０…は５で割り切れるので素数ではない。 ４. ７、１１、１３、１９…と暗記している素数で割る エラトステネスの篩（ふるい）を使う方法 こちらの方法は、中学数学では習わないのですが、 「エラトステネスのふるい」という名の通り、ふるいにかけるように、多くの数のなかから素数を見つけのに便利です。 この方法を使って、1～40までの範囲の素数を見つけてみましょう。 【手順】 １. １を消す ２. 最も小さい素数を残したまま、その素数の倍数をすべて消す。 この場合は、２を残して、２以外の２の倍数をすべてふるい落とします。 ３. 残っている中で最も小さい素数を残したまま、その素数の倍数をすべて消す この場合は、３を残して、３以外の３の倍数をすべてふるい落とします。 ４. 手順３を最後まで繰り返す。 ４はすべてふるい落とされているので、５を残して、５以外の５の倍数をすべてふるい落とします。 最後まで繰り返すと、下図のようになります。 中学のテストでよく出る素数判定問題 中学のテストでは、ある数が素数かどうかを見分ける問いがよく出題されます。 例えば、 問題：101は素数か答えなさい 解答：101の約数は「１」と「１０１」の２つなので、１０１は素数である。 などです。 上記で紹介した方法などを用いて、素数かどうかを見分けます。 中学では覚えておくべき素数 中学の問題では、少なくとも【２,３,５,７,１１,１３,１７,１９】あたりまでの素数を暗記しておくとよいでしょう。 暗記をしておくことで、素数を見分ける問題が楽に解けるようになります。 もちろん、素数はずっと続いていきますので、興味があれば暗記してみても面白いかもしれないですね。 素数に関するよくある質問 ・１は素数じゃないの？ 素数の定義をみてみると、「１とその数以外に約数ををもたない（約数が２つの）自然数」となっています。 たとえば、２の約数は１と２の２つ、７の約数は１と７の２つ。 １は、約数が１自身の１つだけしかないので、素数ではないということになります。 ・なぜ2は素数なのか？ なんとなく、２は偶数だから素数ではない気がしてしまいますが、２は素数です。 ２は、「１」と「２」自身の２つの約数をもつ自然数なので、２は素数となります。 うっかりミスで、２が素数ではないと勘違いしないようにしましょう。 ・素数は無限にあるの？ 素数は無限に存在します。 素数が無数に存在することの証明は、色々な方法でされています。 有名なのは、背理法によるユークリッドの証明です。こちらは紀元前に発見されたものです。 そのほかにも、フェルマー数を用いたゴールドバッハの証明や、2006年に発表されたサイダックの証明などがあります。 ・素数は何年生で学ぶ？ 素数は、中学１年生で学びます。 現行の学習指導要領では、素数を１年において扱うことにより、 素因数分解を自然数、素数、倍数、約数、公倍数、公約数などと関連づけ、 整数の性質を探るひとつの道具として利用することができるとしています。 参考：文部科学省「中学校学習指導要領(平成29年告示)解説」2017年 ▼文部科学省ホームページ 中学校学習指導要領解説：文部科学省 ・100までの素数リストは？ １～１００までに、素数は 「 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97」があり、全部で25個あります。 下図の白い背景のマスが、素数です。 素数の面白い応用例 素数は、とても不思議な数字です。 身近でも、素数の面白い応用例や、素数に絡んだ不思議なことがたくさんあります。 インターネットの暗号に使われる素数 インターネット上の情報を守るのに「暗号化」という技術が使われていますが、この暗号化において素数が重要な役割を担っています。 とある文書があったとき、素数×素数のかけ算で文書に暗号をかけます。 第三者には、かけ算の結果が公開されています。 暗号を元の文書に戻すためには別の鍵が必要です。 この鍵を得るためには、自然数＝素数×素数と、逆の計算をしなければいけません。 地道に計算するので、素数の桁が大きいほど大変です。 簡単な例で考えると、１９×２３のかけ算はひっ算を使えばすぐできるけど、437＝19×23を逆の計算をするのは大変ですよね。 この作業は、コンピューターでも膨大な時間がかかるため、インターネットのセキュリティでは素数が重要な役割を担っているということです。 自然界の不思議：セミと素数の関係 素数ゼミとよばれるセミを聞いたことがあるでしょうか。 素数ゼミとは、生き残り戦略のために、１３年、もしくは１７年の間、地中にいるセミのことです。 それでは、なぜ素数である１３年、もしくは１７年の間、地中にいることが生き残り戦略となるのでしょうか。 その秘密は、最小公倍数にあります。 例えば、１３年ゼミ周期で土の中から出てくる素数ゼミに、３年周期で発生する天敵がいたとします。 天敵が３年周期で発生していても、同じ年に１３年周期ゼミが地上に出るのは、上の表のように３９年経ったときのみです。 ３９は、１３と３の最小公倍数です。１３が素数であるため、３を約数に持たないことから、この最小公倍数が大きくなっています。 仮にセミの地上にいる期間が１年短い１２年だとすると、地上に出れば毎回３年周期で発生している天敵がいるということになってしまいます。 セミの発生周期が素数であることは、その数自身しか約数がない自然数である素数を地上にでる周期にすることで、 天敵とできるだけ出会わないようにする、セミの生き残り戦略と考えることができます。 「わからないをわかるにかえる数学」 ここでPR！ 今回解説した「素数」は中学１年生で学びます。 そんな中学生向けの中学生向けの超基礎シリーズが、こちらの『わからないをわかるにかえる』。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▶シリーズページはこちら ▶ご購入はこちら 「わからないをわかるにかえる高校入試数学」 人気の超基礎シリーズ「わからないをわかるにかえる」の高校入試対策版です。 中学3年間の内容を基礎からおさらいできます。 やさしい言葉遣いやイラストで、とっつきやすいのが特徴で、苦手な分野が多く、易しめから入りたい人はチェックしてみてください。 ▶シリーズページはこちら ▶ご購入はこちら 「大人の教科書ワーク 数学」 日常の悩みや疑問を、小中学校の教科書で解決！ それがこちらの『大人の教科書ワーク』です。 実は、今回の記事のなかで紹介した「インターネットの暗号に使われる素数」や「セミと素数の関係」について、 この『大人の教科書ワーク数学』ではさらに詳しく書かれています！ この本では、このような数学にまつわる面白いトピックをたくさんとりあげています。 「大人の学び直し」がテーマの本ですが、小中学校の教科書で習う算数・数学の内容を用いながら、 日常のあらゆる疑問に答える形式になっているので、いままさに数学を学んでいる中学生が数学を学ぶ楽しさを知るのにもぴったりです！ ▶シリーズページはこちら ▶ご購入はこちら まとめ いかかでしたか。 今回の記事では、素数の定義から中学数学で押さえておきたいポイント、素数を応用した例までご紹介しました。 素数は数学の基礎であると同時に、どこか不思議な数字ですよね。 素数を通じて数学の魅力に触れ、ぜひ今の学びを深めてみてください！
中学数学の公式をわかりやすくまとめます！高校入試にも役立つ完全ガイド
もくじ はじめに 中学数学で覚えるべき公式とは？ 高校入試で役立つ公式 「なぜそうなるか」から数学公式を理解する 覚え方・使いこなし練習 おすすめの学習教材 まとめ はじめに 「数学の公式って、たくさんあって覚えきれないな…」 「高校入試に向けて、どの公式をしっかり押さえておけばいいんだろう？」 そんな悩みを解消するために、今回は中学数学で学ぶ公式を解説します！ 公式を「知る」から「使える」に変えるための完全ガイド、ぜひ最後まで読んでみてくださいね！ 中学数学で覚えるべき公式とは？ 中学3年間で学習する数学は、主に計算（方程式）、関数、図形の3つの分野に分類できます。 ※データの活用もありますが、今回は公式ということで省略します。 一見するとバラバラに見えるかもしれませんが、実はどれも深いところでつながっています。 学年ごとに確認しましょう。 中1で習う数学公式のポイント 中学1年生になると、算数から数学に教科名が変更され、本格的な数学の学習が始まります。 中学1年生で学習する公式は、この先の数学の土台になりますのでしっかり理解しましょう。 ◆ 正の数・負の数【計算】 四則演算（たし算、ひき算、かけ算、わり算）は、符号ミスに注意することが大切です。 符号の関係を公式としてまとめておくと便利です。 ◆ 文字式【計算】 分配法則は、今後の計算の基本になりますのでここで理解しておきましょう。 割合や速さの関係も、文章題を解く上で大切です。こちらは小学校での学習内容になりますが押さえておきましょう。 ◆ １次方程式【計算】 等式の性質が方程式を解くときの基本になります。移項するときは符号に注意しましょう。 ◆ 比例・反比例【関数】 関係式を公式として整理しましょう。座標の読み取り方も重要です。 ◆ 平面図形・空間図形【図形】 おうぎ形の面積、立体の体積を公式として覚えておきましょう。 おうぎ形は円の一部分だとイメージすると、計算するときに式を思い出しやすくなります。 中2で習う数学公式のポイント 中学2年生では、さらに一歩進んだ内容を学習します。 図形の単元で証明を学習し、ものごとを順序だてて説明する力を養います。 図形に関する公式（定義や定理）が増えますので、正確に理解する力が求められます。 ◆ １次関数【関数】 y=ax+b の形と式の意味、変化の割合などを覚えましょう。高校入試や定期テストでは、図形問題に応用されることも多いです。 ◆ 平行と合同【図形】 平行線と角の関係や、多角形の内角の和・外角の和は、入試の図形問題を解く際にも重要な内容です。 三角形の合同条件は、証明問題を解く際、数多く出てきます。 ◆ 特別な四角形【図形】 平行四辺形、長方形、ひし形、正方形の定義や性質は、小学校で学習した内容でもあります。 中学２年生では、定義、定理として再確認します。 中3で習う数学公式のポイント 中学3年生で学習する公式は、高校入試に直結する重要なものが多くあります。 特に平方根、２次方程式、相似、円、三平方の定理は、入試の頻出単元として強調しておきたいポイントです。 ◆ 多項式【計算】 展開や乗法公式、因数分解の公式が出てきます。因数分解は、２次方程式を解くときにも役立ちます。 ◆ 平方根【計算】 無理数（分数で表すことのできない数）へと数の世界が広がる面白い単元です。 新しい記号であるルートの計算方法を、公式として押さえておきましょう。 ◆ ２次方程式【計算】 主に３つの解き方があります。 因数分解を利用した解き方、解の公式を覚えておくと安心です。 ◆ 相似【図形】 三角形の相似条件は、合同条件との違いを意識して覚えましょう。 線分の比の関係、面積比、体積比は、入試でよく問われます。 ◆ 円【図形】 円や弧を見つけたら、円周角の定理を意識しましょう。 半円の弧に対する円周角が直角(90°)であることも覚えておくと便利です。 ◆ 三平方の定理【図形】 直角三角形の辺の長さの関係を表す定理です。 高校入試頻出で、関数もふくめ、多くの問題で応用されます。 高校入試で役立つ公式 高校入試でよく出る公式を厳選しました。 これらを重点的にマスターし、入試本番で得点アップを目指しましょう。 入試でよく出題される公式には理由があります。 それは、単に知識を問うだけでなく、複雑な問題を解く際に利用したり、他の単元にも応用できるからです。 それでは順番に見ていきましょう。 1. 三平方の定理 図形問題で辺の長さを求めるときに必須です。 平面図形だけでなく、関数や空間図形にも応用されます。 長さを求める問題が出てきたときは、三平方の定理が使えないか意識しましょう。 図形の中にひそむ直角三角形を見つけることがポイントです。 2. ２次方程式の解の公式 因数分解を利用して解けない方程式でも解ける万能な公式です。 因数分解が思いつかなくても焦らなくなります。 3. 関数とグラフの式 直線の式（１次関数の式） y=ax+b 放物線の式 y=ax2 双曲線 y= x a グラフから式や座標を求める問題は頻出です。 グラフの特長と式の形を整理しておきましょう。 比例y=axのグラフは原点を通る直線ですので、１次関数でb=0のときと覚えておくと便利です。 4. 展開・因数分解の公式 単問の計算問題だけでなく、文章題で式をつくった後の計算で利用することもあります。 ２次方程式を解く際にも役立ちます。 5. 合同条件・相似条件 図形の証明問題で必須です。減点対象にもなるので、正確に書けるように覚えましょう。 辺の長さを求めるときに、図形が合同、相似であることを利用する場合もあります。 6. 円周角の定理 円に関する図形問題で、角度を求めるときによく使われます。 図形の中に円や弧を見つけたら、円周角の定理を意識して角度を調べてみましょう。 7. 多角形の内角の和・外角の和 基本的な図形問題や証明問題で使われます。 どんな多角形でも外角の和は360°ですので、外角から考えると計算しやすくなる場合もあります。 入試での使われ方と注意点 高校入試では、公式をただ覚えているだけでは点数につながりません。 公式が「どんなパターンで出題されるか」を知り、「使いこなす力」を身につけることが何よりも重要です。 例えば、三平方の定理は、関数や空間図形の中に隠れていることもあります。 公式を使えるようになるために、様々な問題を解くことが何よりも大切です。 また、一つの問題で複数の公式を組み合わせるパターンもよく出題されます。 公式を単独で覚えるだけでなく、それぞれの公式がどう連携し合っているのか、全体像を意識して学習に取り組みましょう。 「なぜそうなるか」から数学公式を理解する 公式を丸暗記するだけでは、少し問題がひねられると対応できなくなってしまいます。 公式が「なぜそうなるのか」、その成り立ちを理解することで、忘れにくく、応用も効く「使える知識」になります。 • ２次方程式の解の公式 なぜあの複雑な形になるのか？ これは平方完成という考え方から導き出されます。 式の変形を順を追って理解することで、公式がより深く頭に残ります。 • 三平方の定理 なぜ a2+b2=c2 なのか？ これは、直角三角形の各辺を一辺とする正方形の面積の関係を表しています。 図を使って考えることで、視覚的に理解を深められます。 • 円周角の定理 なぜ「中心角の半分になる」のか？ これは補助線をひいて、二等辺三角形の性質を使うと、簡単に証明できます。 このように、「なぜ？」という疑問を持つことは、数学の面白さを発見する第一歩です。 公式を使って問題をたくさん解くとともに、その公式がなぜ成り立つのか調べてみると理解が深まります。 覚え方・使いこなし練習 公式を覚えるには、ただ眺めているだけでは不十分です。 効果的な覚え方と、実際に使いこなすための練習法を知ることが、記憶定着と応用力アップのカギとなります。 語呂合わせ・図解を活用しよう 文字ばかりの公式を覚えるのが苦手なら、語呂合わせや図解を積極的に活用しましょう。 例えば、球の表面積や体積の公式などは語呂合わせがあります。 ・球の表面積は、「心配（4π）あるある（r2）」 ・球の体積は、「身の上に心配（ 4π 3 ）あるから参上（r3）」 公式を覚えるときに、自分だけの語呂合わせをつくってみましょう。 友達と共有しても面白いかもしれません。 円周角の定理などは、図で視覚的に理解する方が記憶に残りやすいです。 図解が必要な公式は、自分で簡単な絵をかいたり、教科書や参考書の図をじっくり見たりして、「なぜこうなっているんだろう？」と考えてみましょう。 視覚を利用して覚えることで、いざという時に「あの図だ！」と思い出しやすくなります。 公式を使う練習のすすめ 公式は、問題演習とセットで覚えることが記憶定着のコツです。 覚えた公式を、実際に問題を解きながら使ってみることで、その使い方や、どんな時に使うべきかが自然と身につきます。 間違えた問題は、なぜ間違えたのか、どの公式の使い方が間違っていたのかをしっかり確認し、もう一度解き直しましょう。 この繰り返しが、公式を「使える力」に変える最も効果的な方法です。 おすすめの学習教材 公式の理解と定着を深めるためには、適切な教材選びも重要です。 ここで、皆さんの学習を強力にサポートしてくれる教材をご紹介します。 ◆ 中学教科書ワーク 学校の教科書の内容に沿ってつくられているため、日々の授業の予習・復習に最適です。 イラストや図解が豊富で、数学の公式も詳しく解説されています。 高校入試に有効な問題も多くふくまれており、基礎から応用まで着実に力をつけることができます。 ▶シリーズページはこちら ▶ご購入はこちら ◆ わからないをわかるにかえる ニガテなところがどんどんわかる！超基礎からやさしく学べる、中学生のための問題集！ 数学の基本的な問題の解き方を丁寧に解説しています。 公式も覚えやすくなるよう配慮していますので、数学が苦手な方でも大丈夫。 小学生の先取り学習や、高校生・大人の学び直しにもおすすめです。 学年別・領域別と、高校入試シリーズがあります。 ▶シリーズページはこちら ▶ご購入はこちら ◆ 完全攻略 教科書だけではもの足りないキミに送る、定期テスト対策から高校入試の基礎固めに最適な問題集です。 ▶シリーズページはこちら ▶ご購入はこちら ◆ ハイクラス徹底問題集 最高峰の問題演習で、「試験に強い実力」をつけられる問題集です。レベルの高い問題にチャレンジしたい方に最適です。 ▶シリーズページはこちら ▶ご購入はこちら まとめ 公式を「使える力」に変えよう ここまで、中学数学の公式について、その種類から高校入試での重要性、そして効果的な学習法まで、幅広く紹介してきました。 大切なのは、公式を「知る」→「理解する」→「使えるようになる」という段階をしっかり踏むことです。 丸暗記ではなく、「なぜそうなるのか」を考え、実際に問題を解きながら使いこなす練習を続けましょう。 それが、数学の力を大きく伸ばすカギとなります。 紹介した文理の教材をうまく活用し、公式を「使える力」に変えて、自信を持って高校入試に挑んでくださいね。 皆さんの学習がより充実したものになるよう、心から応援しています！
