中学数学の公式をわかりやすくまとめます!高校入試にも役立つ完全ガイド

はじめに
「数学の公式って、たくさんあって覚えきれないな…」
「高校入試に向けて、どの公式をしっかり押さえておけばいいんだろう?」

そんな悩みを解消するために、今回は中学数学で学ぶ公式を解説します!
公式を「知る」から「使える」に変えるための完全ガイド、ぜひ最後まで読んでみてくださいね!
中学数学で覚えるべき公式とは?
中学3年間で学習する数学は、主に計算(方程式)、関数、図形の3つの分野に分類できます。
※データの活用もありますが、今回は公式ということで省略します。
一見するとバラバラに見えるかもしれませんが、実はどれも深いところでつながっています。
学年ごとに確認しましょう。
中1で習う数学公式のポイント
中学1年生になると、算数から数学に教科名が変更され、本格的な数学の学習が始まります。
中学1年生で学習する公式は、この先の数学の土台になりますのでしっかり理解しましょう。
◆ 正の数・負の数【計算】
四則演算(たし算、ひき算、かけ算、わり算)は、符号ミスに注意することが大切です。
符号の関係を公式としてまとめておくと便利です。

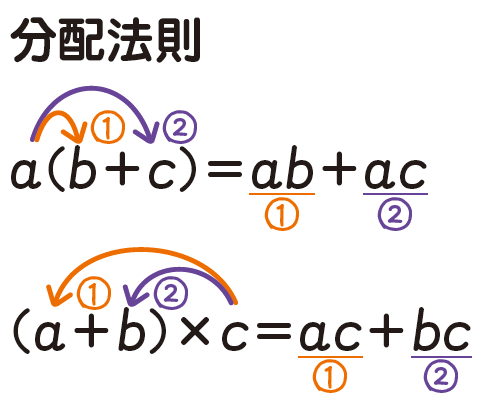
◆ 文字式【計算】
分配法則は、今後の計算の基本になりますのでここで理解しておきましょう。
割合や速さの関係も、文章題を解く上で大切です。こちらは小学校での学習内容になりますが押さえておきましょう。
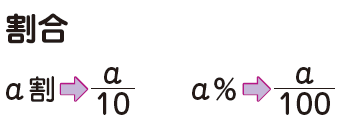

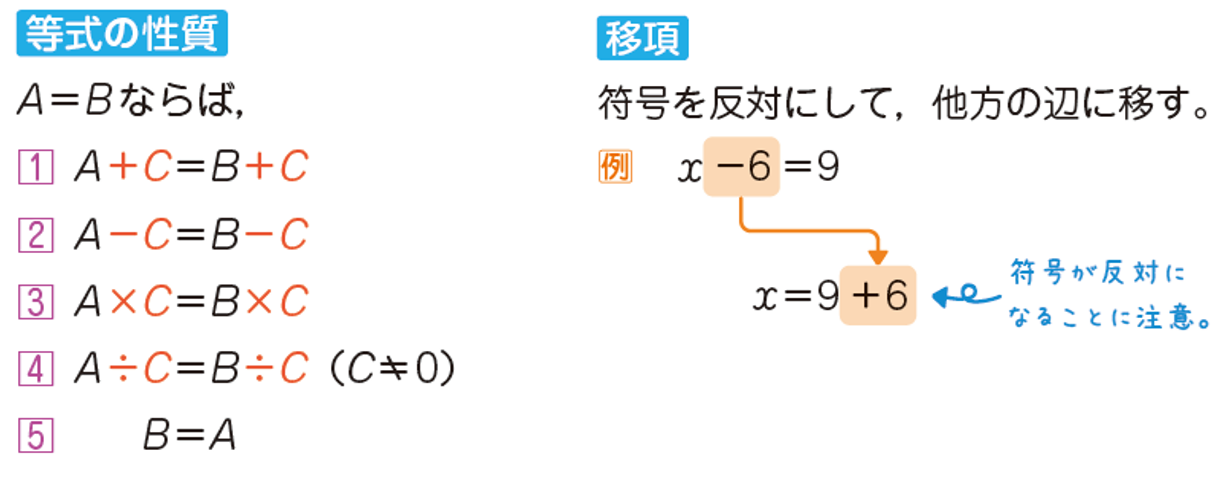
◆ 1次方程式【計算】
等式の性質が方程式を解くときの基本になります。移項するときは符号に注意しましょう。
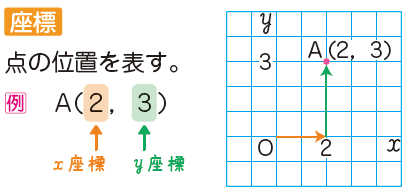
◆ 比例・反比例【関数】
関係式を公式として整理しましょう。座標の読み取り方も重要です。

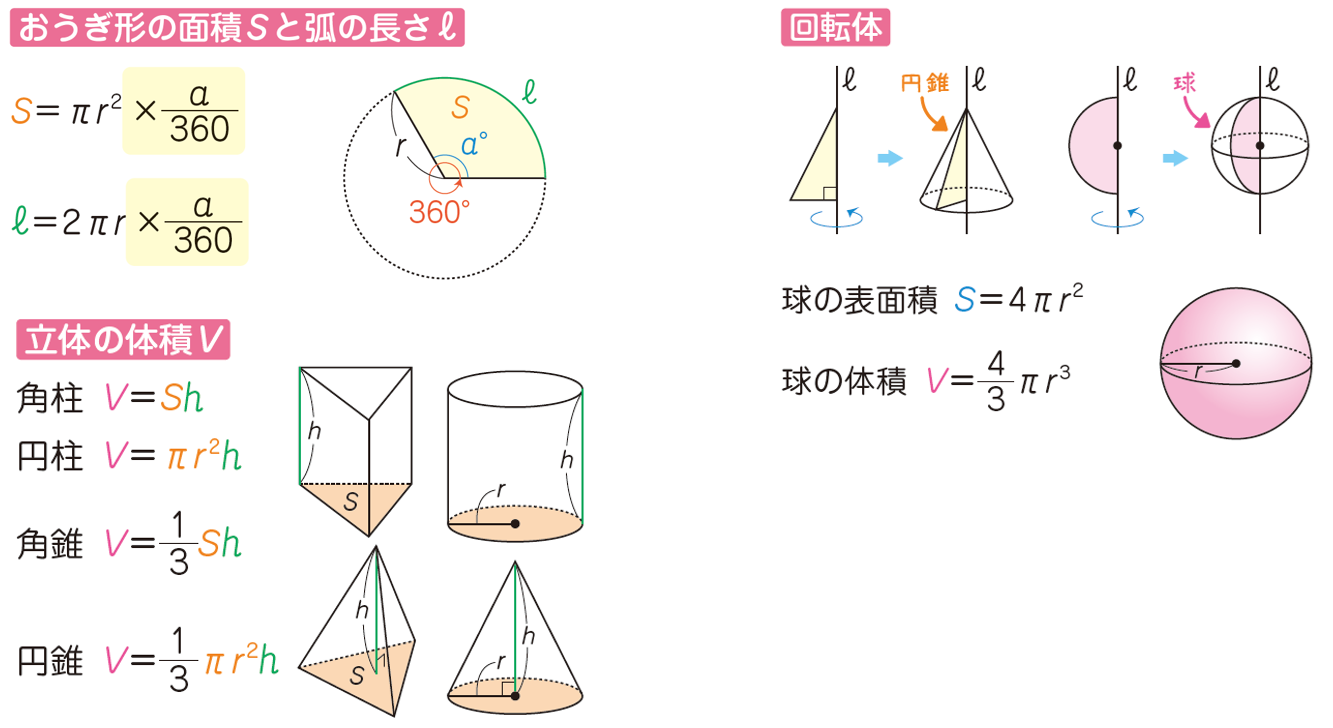
◆ 平面図形・空間図形【図形】
おうぎ形の面積、立体の体積を公式として覚えておきましょう。
おうぎ形は円の一部分だとイメージすると、計算するときに式を思い出しやすくなります。
中2で習う数学公式のポイント
中学2年生では、さらに一歩進んだ内容を学習します。
図形の単元で証明を学習し、ものごとを順序だてて説明する力を養います。
図形に関する公式(定義や定理)が増えますので、正確に理解する力が求められます。
◆ 1次関数【関数】
y=ax+b の形と式の意味、変化の割合などを覚えましょう。高校入試や定期テストでは、図形問題に応用されることも多いです。

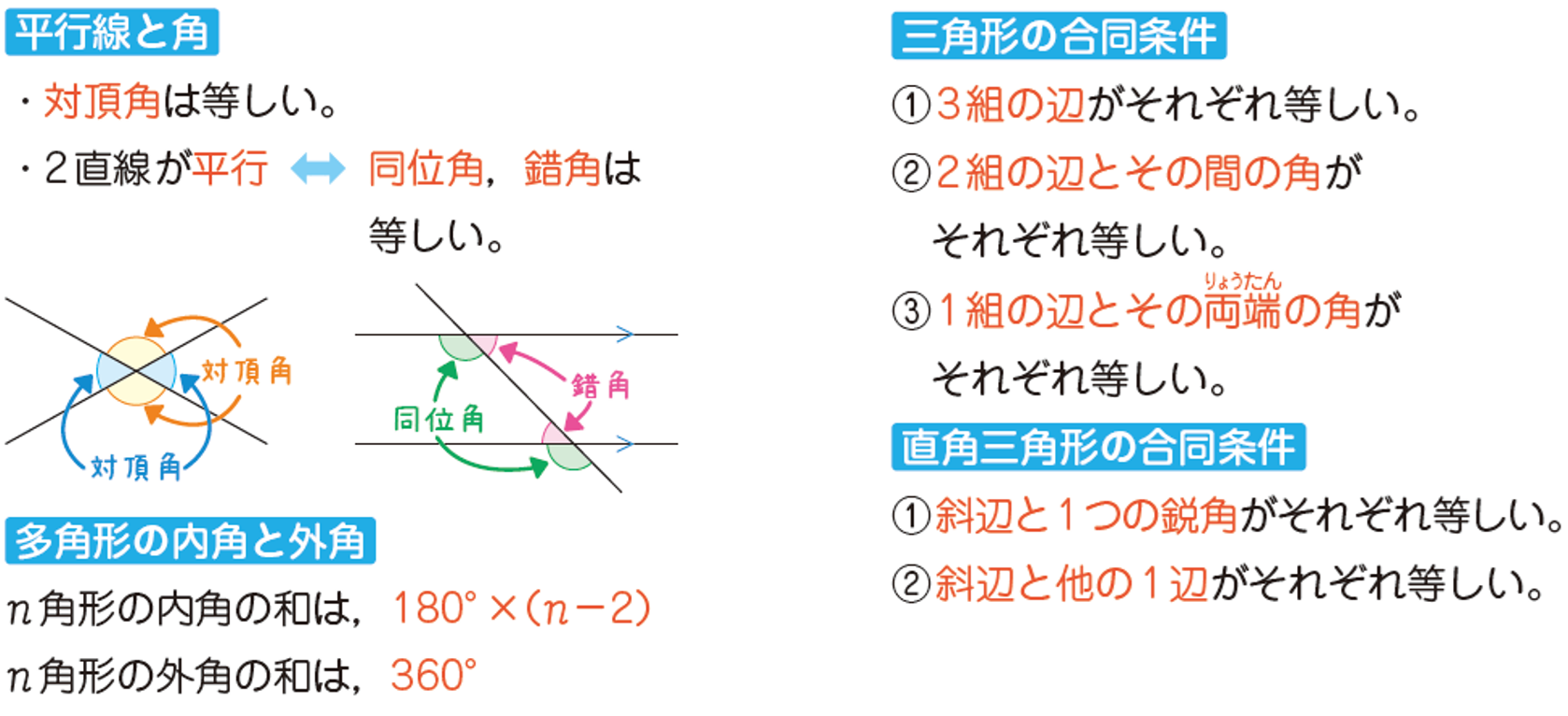
◆ 平行と合同【図形】
平行線と角の関係や、多角形の内角の和・外角の和は、入試の図形問題を解く際にも重要な内容です。
三角形の合同条件は、証明問題を解く際、数多く出てきます。
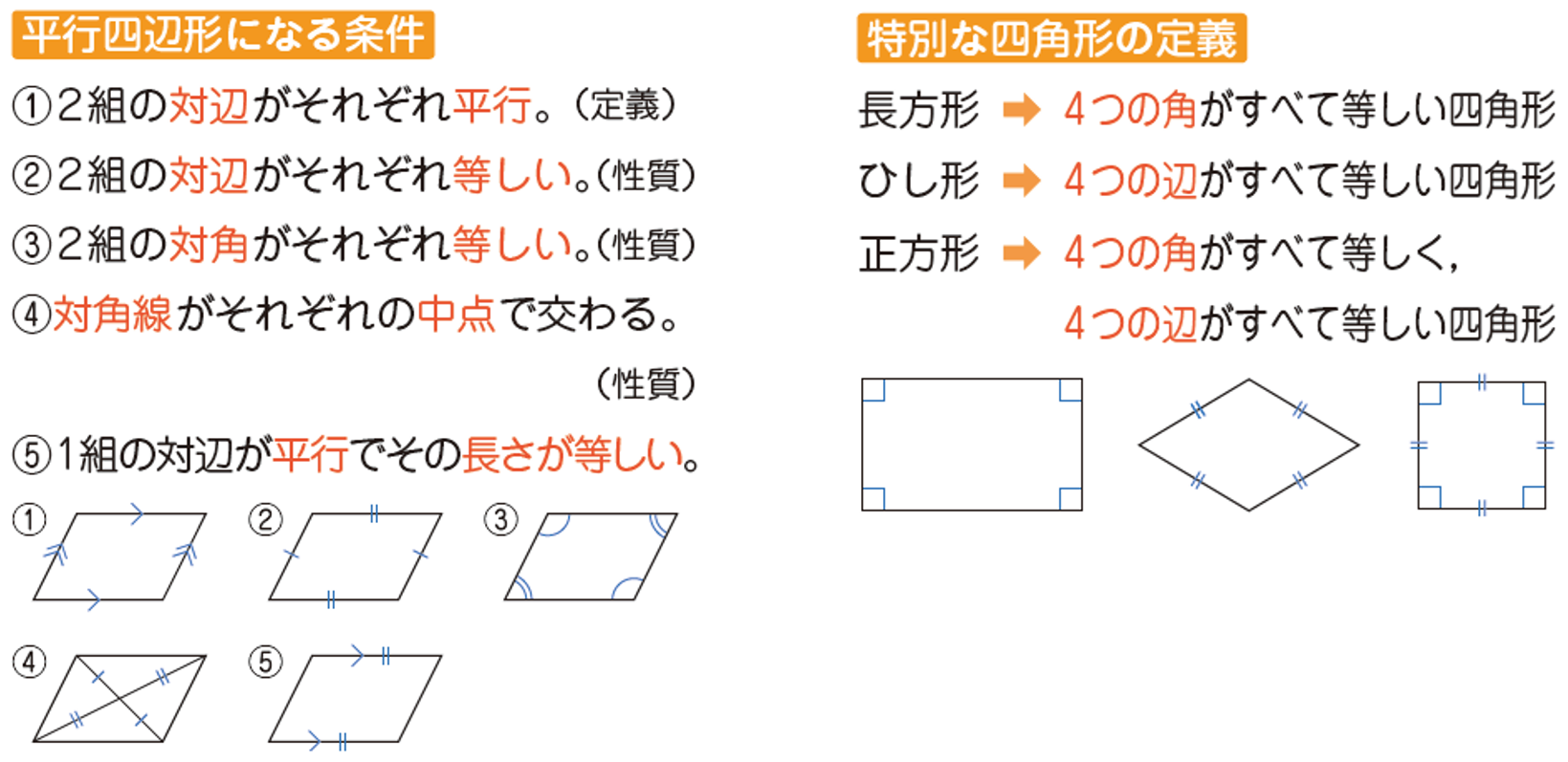
◆ 特別な四角形【図形】
平行四辺形、長方形、ひし形、正方形の定義や性質は、小学校で学習した内容でもあります。
中学2年生では、定義、定理として再確認します。
中3で習う数学公式のポイント
中学3年生で学習する公式は、高校入試に直結する重要なものが多くあります。
特に平方根、2次方程式、相似、円、三平方の定理は、入試の頻出単元として強調しておきたいポイントです。
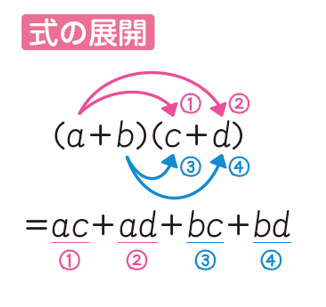
◆ 多項式【計算】
展開や乗法公式、因数分解の公式が出てきます。因数分解は、2次方程式を解くときにも役立ちます。

◆ 平方根【計算】
無理数(分数で表すことのできない数)へと数の世界が広がる面白い単元です。
新しい記号であるルートの計算方法を、公式として押さえておきましょう。

◆ 2次方程式【計算】
主に3つの解き方があります。
因数分解を利用した解き方、解の公式を覚えておくと安心です。


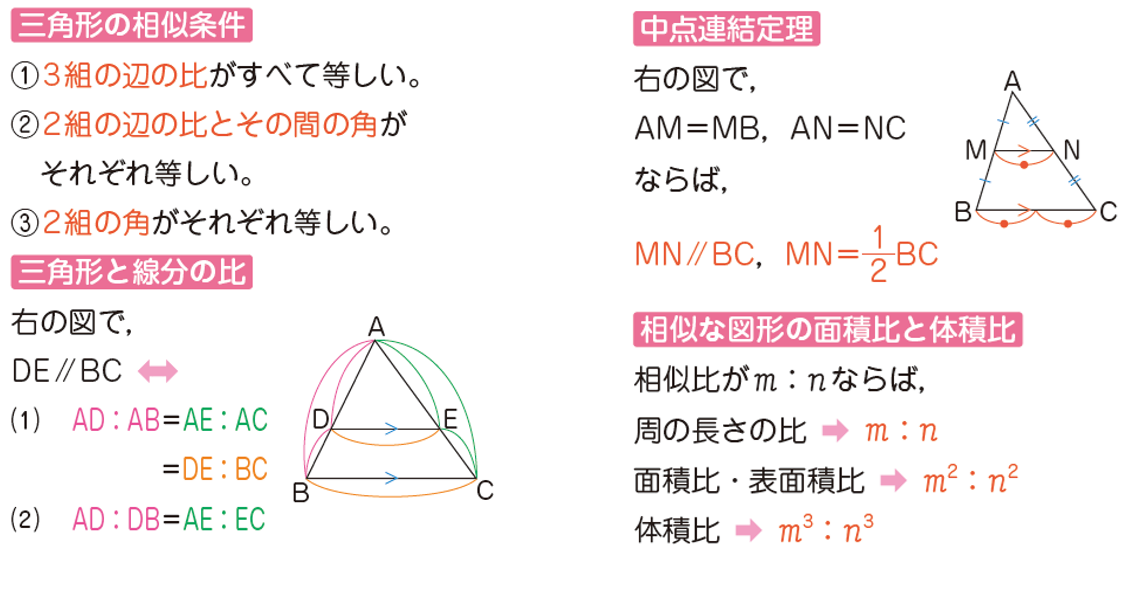
◆ 相似【図形】
三角形の相似条件は、合同条件との違いを意識して覚えましょう。
線分の比の関係、面積比、体積比は、入試でよく問われます。
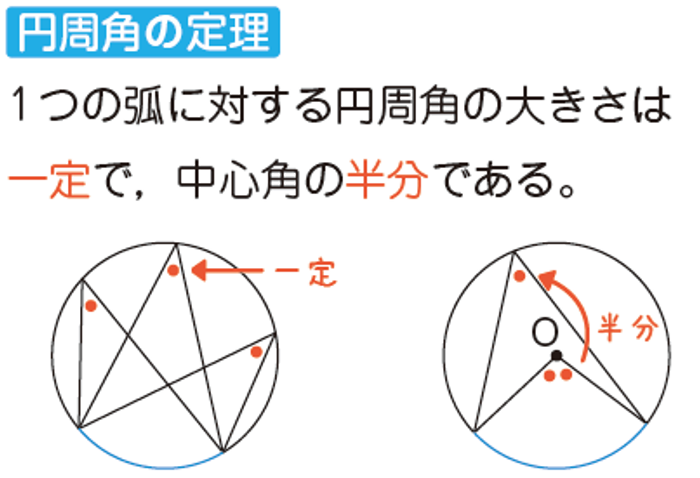
◆ 円【図形】
円や弧を見つけたら、円周角の定理を意識しましょう。
半円の弧に対する円周角が直角(90°)であることも覚えておくと便利です。
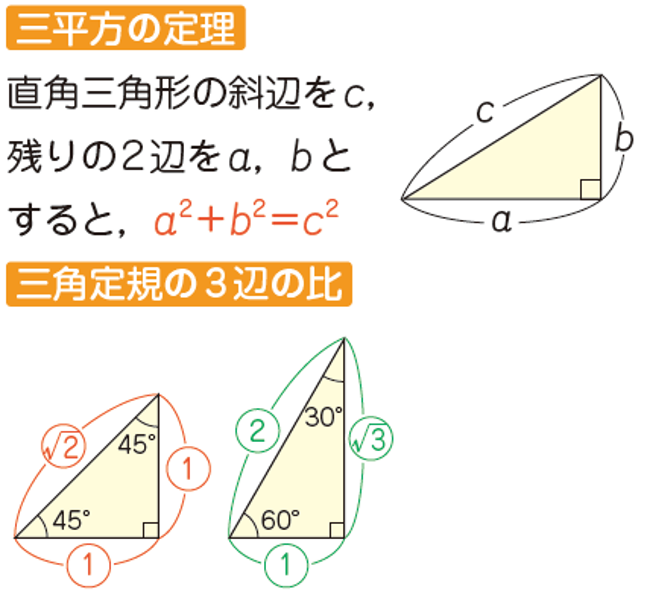
◆ 三平方の定理【図形】
直角三角形の辺の長さの関係を表す定理です。
高校入試頻出で、関数もふくめ、多くの問題で応用されます。
高校入試で役立つ公式
高校入試でよく出る公式を厳選しました。
これらを重点的にマスターし、入試本番で得点アップを目指しましょう。
入試でよく出題される公式には理由があります。
それは、単に知識を問うだけでなく、複雑な問題を解く際に利用したり、他の単元にも応用できるからです。
それでは順番に見ていきましょう。
1. 三平方の定理
図形問題で辺の長さを求めるときに必須です。
平面図形だけでなく、関数や空間図形にも応用されます。
長さを求める問題が出てきたときは、三平方の定理が使えないか意識しましょう。
図形の中にひそむ直角三角形を見つけることがポイントです。
2. 2次方程式の解の公式
因数分解を利用して解けない方程式でも解ける万能な公式です。
因数分解が思いつかなくても焦らなくなります。
3. 関数とグラフの式
直線の式(1次関数の式) y=ax+b
放物線の式 y=ax2
双曲線 y= x a
グラフから式や座標を求める問題は頻出です。
グラフの特長と式の形を整理しておきましょう。
比例y=axのグラフは原点を通る直線ですので、1次関数でb=0のときと覚えておくと便利です。
4. 展開・因数分解の公式
単問の計算問題だけでなく、文章題で式をつくった後の計算で利用することもあります。
2次方程式を解く際にも役立ちます。
5. 合同条件・相似条件
図形の証明問題で必須です。減点対象にもなるので、正確に書けるように覚えましょう。
辺の長さを求めるときに、図形が合同、相似であることを利用する場合もあります。
6. 円周角の定理
円に関する図形問題で、角度を求めるときによく使われます。
図形の中に円や弧を見つけたら、円周角の定理を意識して角度を調べてみましょう。
7. 多角形の内角の和・外角の和
基本的な図形問題や証明問題で使われます。
どんな多角形でも外角の和は360°ですので、外角から考えると計算しやすくなる場合もあります。
入試での使われ方と注意点
高校入試では、公式をただ覚えているだけでは点数につながりません。
公式が「どんなパターンで出題されるか」を知り、「使いこなす力」を身につけることが何よりも重要です。
例えば、三平方の定理は、関数や空間図形の中に隠れていることもあります。
公式を使えるようになるために、様々な問題を解くことが何よりも大切です。
また、一つの問題で複数の公式を組み合わせるパターンもよく出題されます。
公式を単独で覚えるだけでなく、それぞれの公式がどう連携し合っているのか、全体像を意識して学習に取り組みましょう。
「なぜそうなるか」から数学公式を理解する
公式を丸暗記するだけでは、少し問題がひねられると対応できなくなってしまいます。
公式が「なぜそうなるのか」、その成り立ちを理解することで、忘れにくく、応用も効く「使える知識」になります。
• 2次方程式の解の公式
なぜあの複雑な形になるのか?
これは平方完成という考え方から導き出されます。
式の変形を順を追って理解することで、公式がより深く頭に残ります。
• 三平方の定理
なぜ a2+b2=c2 なのか?
これは、直角三角形の各辺を一辺とする正方形の面積の関係を表しています。
図を使って考えることで、視覚的に理解を深められます。
• 円周角の定理
なぜ「中心角の半分になる」のか?
これは補助線をひいて、二等辺三角形の性質を使うと、簡単に証明できます。
このように、「なぜ?」という疑問を持つことは、数学の面白さを発見する第一歩です。
公式を使って問題をたくさん解くとともに、その公式がなぜ成り立つのか調べてみると理解が深まります。
覚え方・使いこなし練習
公式を覚えるには、ただ眺めているだけでは不十分です。
効果的な覚え方と、実際に使いこなすための練習法を知ることが、記憶定着と応用力アップのカギとなります。
語呂合わせ・図解を活用しよう
文字ばかりの公式を覚えるのが苦手なら、語呂合わせや図解を積極的に活用しましょう。
例えば、球の表面積や体積の公式などは語呂合わせがあります。
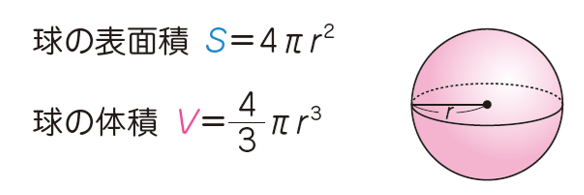
・球の表面積は、「心配(4π)あるある(r2)」
・球の体積は、「身の上に心配( 4π 3 )あるから参上(r3)」
公式を覚えるときに、自分だけの語呂合わせをつくってみましょう。
友達と共有しても面白いかもしれません。
円周角の定理などは、図で視覚的に理解する方が記憶に残りやすいです。
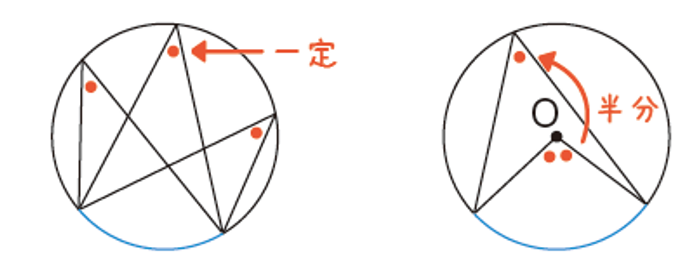
図解が必要な公式は、自分で簡単な絵をかいたり、教科書や参考書の図をじっくり見たりして、「なぜこうなっているんだろう?」と考えてみましょう。
視覚を利用して覚えることで、いざという時に「あの図だ!」と思い出しやすくなります。
公式を使う練習のすすめ
公式は、問題演習とセットで覚えることが記憶定着のコツです。
覚えた公式を、実際に問題を解きながら使ってみることで、その使い方や、どんな時に使うべきかが自然と身につきます。
間違えた問題は、なぜ間違えたのか、どの公式の使い方が間違っていたのかをしっかり確認し、もう一度解き直しましょう。
この繰り返しが、公式を「使える力」に変える最も効果的な方法です。
おすすめの学習教材
公式の理解と定着を深めるためには、適切な教材選びも重要です。
ここで、皆さんの学習を強力にサポートしてくれる教材をご紹介します。
◆ 中学教科書ワーク
学校の教科書の内容に沿ってつくられているため、日々の授業の予習・復習に最適です。
イラストや図解が豊富で、数学の公式も詳しく解説されています。
高校入試に有効な問題も多くふくまれており、基礎から応用まで着実に力をつけることができます。

◆ わからないをわかるにかえる
ニガテなところがどんどんわかる!超基礎からやさしく学べる、中学生のための問題集!
数学の基本的な問題の解き方を丁寧に解説しています。
公式も覚えやすくなるよう配慮していますので、数学が苦手な方でも大丈夫。
小学生の先取り学習や、高校生・大人の学び直しにもおすすめです。
学年別・領域別と、高校入試シリーズがあります。


◆ 完全攻略
教科書だけではもの足りないキミに送る、定期テスト対策から高校入試の基礎固めに最適な問題集です。


◆ ハイクラス徹底問題集
最高峰の問題演習で、「試験に強い実力」をつけられる問題集です。
レベルの高い問題にチャレンジしたい方に最適です。

まとめ
公式を「使える力」に変えよう
ここまで、中学数学の公式について、その種類から高校入試での重要性、そして効果的な学習法まで、幅広く紹介してきました。
大切なのは、公式を「知る」→「理解する」→「使えるようになる」という段階をしっかり踏むことです。
丸暗記ではなく、「なぜそうなるのか」を考え、実際に問題を解きながら使いこなす練習を続けましょう。
それが、数学の力を大きく伸ばすカギとなります。
紹介した文理の教材をうまく活用し、公式を「使える力」に変えて、自信を持って高校入試に挑んでくださいね。
皆さんの学習がより充実したものになるよう、心から応援しています!
