2025/11/07
【中学生向け】 数学の解法まとめ！ 高校受験で点が取れるパターン学習法
はじめに：数学の「解法」って何？なぜ大事なの？
「公式はしっかり覚えているのに…」
テストや模試になると、『どうやって解き始めれば良いか思いつかない…』
高校受験の数学で、こんな壁にぶつかっている人が多いのではないでしょうか。
「解き方が思いつかない」原因は、あなたの理解不足ではありません！
それは…
公式を覚えるだけの学習から、
「解法力」を身につける学習に切り替えるタイミング
が来ているサインです。
★ 数学の「解法」とは？ ★
数学における「解法」とは、簡単に言うと、
【問題を解くための決まったやり方や道筋（みちすじ）】
のことです。
数学の問題は、公式や定理をただ暗記しているだけでは通用しません。
特に高校入試では、複数の公式を組み合わせたり、図形に補助線をひいたりといった「最初の一歩」が肝心です。
この「最初の一歩」や「手順」が、数学における解法＝定石（じょうせき）と呼ばれます。
★ 高校入試で点が取れる「定石」とは ★
高校入試で出題される問題の多くは、見た目が複雑に見えても、その裏には「この条件があれば、この手順で解ける」という決まったパターンがあります。
これが「定石」です。
定石を理解し、使えるようになれば、あなたは以下のような壁にぶつかることがなくなります。
・「頭が真っ白になる」 のを防げる！
→ 問題文を見た瞬間に、この定石が使えそうなどと判断できるため
・「時間が足りない」 を防げる！
→ 途中で迷ったり、無駄な計算をしたりする時間がなくなるため
この「定石を思いつく力」こそが解法力であり、高校入試で安定して点を取るために最も大切な力なのです！
次のセクションでは、この解法力を身につける具体的な学習ステップを見ていきましょう。
解法を身につける3ステップ学習法
数学の解法力を身につけるためには、
「見る」「わかる」「使う」
の3つのステップで体系的に学習を進めることが重要です。
ただ解説を読んで暗記するのではなく、この3ステップを踏むことで、家庭学習でも入試に通用する再現性の高い実力を身につけることができます。
【ステップ1】 定番の解法パターンを「見る」
数学の問題には、
「こういう条件があるときは、こう解く」
という決まった「型」があります。
まずは、その型がどんなものかを知るために、定番のパターンを意識的に「見る」ことから始めましょう。
【目的】
問題と解法の「対応パターン」を認識する。
【アクション】
１．教科書や問題集の例題、基本問題を用意します。
２．解き方がすぐにわからなかった問題や、応用問題の導入部分に注目します。
３．問題の「条件（何が与えられているか）」と、解説の「最初の一手（解き始め）」に集中し、
「こういうときは、こう解く」という対応パターンを確認します。
４．付箋（フセン）などを使って、
「比の問題」「面積を求めるときに補助線をひく問題」
など、解法パターンごとに問題を分類していくと、頭の中で整理しやすくなります。
このステップでは、まだ自力で解こうとしなくて大丈夫です。
まずは、
「こういう型があるんだ！」
ということを目で見て理解し、脳にインプットしましょう。
【ステップ2】 なぜそう解くのか「わかる」
ステップ1で「型」を見た後、次に大切なのは「なぜその手順なのか？」という理由を理解する＝「わかる」ことです。
これが、解法をただの暗記で終わらせないための重要なプロセスです。
【目的】
解法の本質を理解し、「応用力」をつける。
【アクション】
解説を読みながら、
「なぜこの補助線をひくのだろう？」
「なぜここで連立方程式にするのだろう？」
と、立ち止まって疑問を持つ習慣をつけましょう。
キーワードは「なぜ」です。
参考書や授業で先生から教わった解説を、自分の言葉でノートに書き直す練習をしましょう。
「この式にする理由は、面積が等しいからです。」
のように、手順だけでなく理由を併記します。
図形問題であれば、定理の名前だけでなく
「この定理を使うと、この角度とこの角度が等しいことが証明できる」
という、使い道の流れを理解するように努めます。
解法の「理屈」がわかれば、問題の数字や設定が変わっても、正しい手順を応用できるようになります。
【ステップ3】 覚えた型を「使う」
最後に、ステップ1と2で理解した解法パターンを、自分の実力として定着させるために「使う」練習をします。
【目的】
定着した解法を、本番で自力で「再現」できる力を養う。
【アクション】
１．自力で解く
ステップ1で見た問題を、もう一度自力で解いてみます。
２．初手だけ見て再トライ
もし途中で手が止まってしまったら、「最初のアクション」だけ解説で確認し、すぐに解説を閉じます。
３．最初からやり直す
最初の一手を見てもなお解き進められない場合は、その解法がまだ定着していないサインです。
すぐに最初からやり直し、解法の流れを意識しながら解き進めます。
４．再現ノートの活用
解法を見てもスムーズに解けなかった問題は、「再現ノート」に書き残し、手順と理由を整理します。
これが、あなたの自分専用の解法集となります。
このステップで大切なのは、「最初の一歩（解法パターン）」を自分の手で再現できるまで繰り返すことです。
単元別：入試によく出る「定番の解法パターン」
ここでは、中学数学の主要な単元で、高校入試によく出題される「解法の定石」を具体的に見ていきましょう。
【方程式の文章題】 手順に従って式をつくり、答えを求める！
文章題は、数学的な思考力と日本語の読解力が試されますが、解き方の流れは決まっています。
定石
１．求める数量を文字で表す
問題で聞かれている数量をxやyなどの文字で表します。
通常は、求めるべき数量を文字で表します。
そうすることで、求めた解をそのまま答えにできるからです。
２．方程式をつくる
文章中の数量の関係（「合計」「等しい」「差」など）に着目し、方程式や連立方程式をつくります。
式をつくりにくいときは、表に整理すると、数量の関係や単位が明確になります。
問題文の数値部分に線をひいて、関係を確かめるのも良いでしょう。
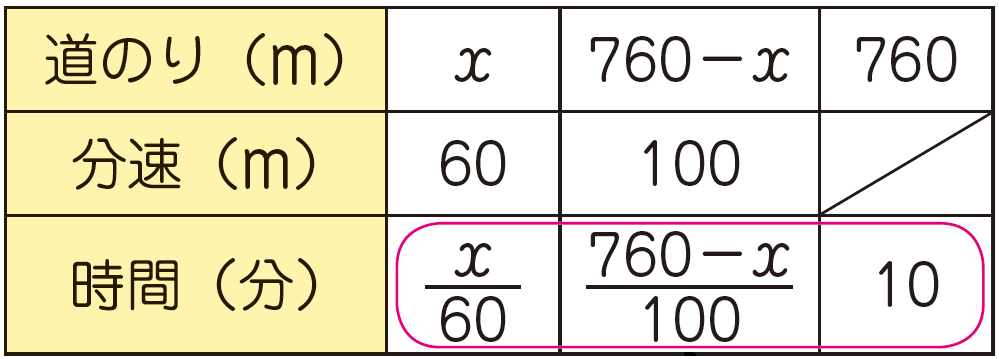
３．解を求めて吟味（ぎんみ）する
２でつくった方程式の解を求めた後、そのまま答えとして良いか確かめます。
問題の条件を満たしているかを確認し、単位をつけて答えをかきます。
要注意：人数を求めるのに、答えが小数や分数になっていないか
金額を求めるのに、答えが負の数になっていないか
など、問題に当てはまるかを考えましょう。
間違いやすいポイント
割合 → 百分率は小数に直してから計算
例 x円の 20% 引き
→ (1－0.2)x
速さ → 単位をそろえてから計算
例 行きは 2時間、帰りは 30分 かかった。
→ 合計の時間は、
2+0.5 (時間) または、 120+30 (分)
【関数】 グラフ・表・式をつなげる解き方
関数の解法の定石は、グラフ、表、式の3つの関係をおさえ、自由に変換できるようにすることです。
定石
１．表から式をつくる
変化の割合やxとyの値の関係から、
・yがxに比例、反比例しているのか
・1次関数か
・xの2乗に比例しているか
を見抜き、式に表します。
２．式からグラフをかく
中学校で学習する関数のグラフには、直線と曲線があります。
式が y=ax+b と、1次関数（ b=0 のときは比例）の形をしていたら、傾きと切片からグラフをかきます。
式が y= x a 、y=ax2 の形をしていたら、xに 1 、 2 、 3 … のときの値を代入して座標を求め、
それぞれの点を通るような、なめらかな曲線をかきます。
３．交点の座標の求め方（連立方程式の利用）
グラフの交点の座標を求めるときは、それぞれのグラフの式から連立方程式をつくって解くのが定石です。
・2直線の交点
→ y を消去して、 x についての１次方程式を解きます。
・x軸との交点
→ x軸は y=0 の直線と考えます。
グラフの式に y=0 を代入し、xの値を求めます。
・放物線（ y=ax2 ）と直線の交点
yを消去して、xについての2次方程式を解きます。
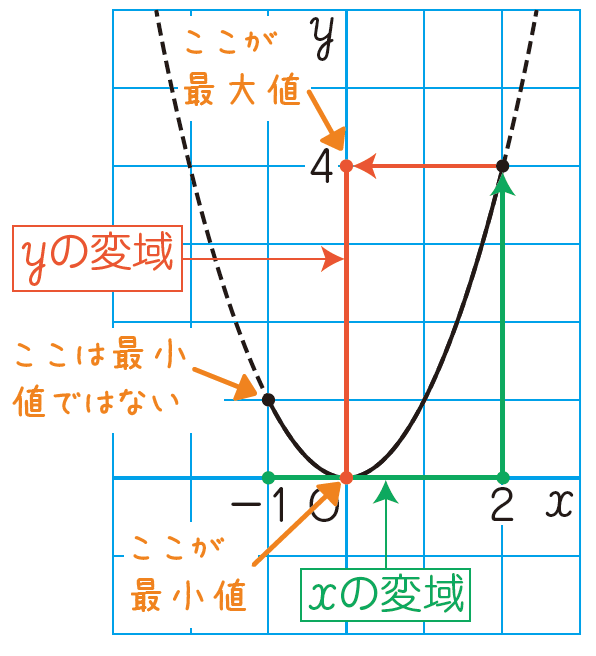
間違いやすいポイント
y=ax2 の変域を求めるとき、原点Oをまたぐ変域になっているときは要注意です。
yの変域の最小値や最大値が 0 になることに気づかないミスが多いです。
【図形】 合同・相似・角度の見抜き方
図形問題では、「補助線をひく場所」や「どの三角形に注目するか」というパターンの見分け方が定石となります。
定石
１．補助線をひく
平行線や接線、円周角など、問題の条件から定理を利用できるように補助線をひくのが定石です。
２．特別な図形に注目
与えられた図形の中に、合同な三角形や相似な三角形、二等辺三角形などの特別な図形が隠れていないかを見抜くことが重要です。
３．錯角・同位角の利用
平行線が示されている場合、錯角・同位角が等しいことを利用して角度を求めたり、相似の証明につなげたりします。
間違いやすいポイント
合同と相似の条件を混同しないようにしましょう。
証明問題で、根拠となる定理や条件（例：平行線の錯角など）を明確に記述せずに進めてしまわないようにしましょう。
【確率】 場合分けと樹形図の使い方
確率の問題は、数え忘れや重複をさけて、すべての場合の数を正確に把握することが定石となります。
定石
・さいころを2つ使うなど、事象が2つで独立している場合は、表にまとめると便利です。
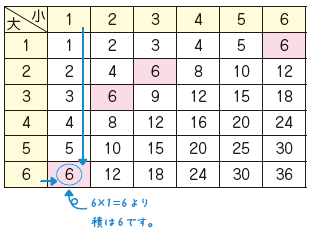
・玉を順番に取り出す場合や、じゃんけんのように順番や組み合わせが複雑な場合は、樹形図を使って数え漏れをふせぎます。
１．表や樹形図で整理する
２．すべての場合の数を求める
樹形図や表のマス目を数え、起こりうる全ての場合の数を求めます。樹形図は小さい順に、規則正しく書いていくのが鉄則です。
３．問題の条件を満たす場合の数を求める
その中で、問題の条件に当てはまる場合の数を数えます。
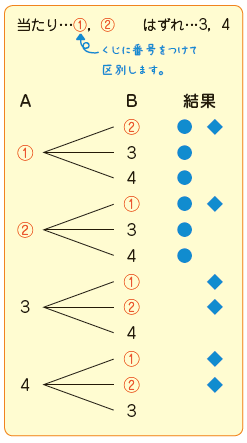
間違いやすいポイント
さいころ2個のように「区別がない」ように見えても、それぞれ「大・小」として区別して全ての場合の数を数え上げる場合が多いです。
どのようなサイコロやコインを使っているのか、問題文をよく読むようにしましょう。
解法暗記は必要？ 暗記だけじゃない勉強法
高校受験の勉強法について調べると、
「数学は暗記するな、理解しろ」
という意見と
「解法はパターンとして暗記すべきだ」
という意見の両方を目にします。
いったいどちらが正しいのでしょうか。
結論から言うと、どちらも大切ですが、順番が重要になります。
数学で本当に実力をつけるには、以下のサイクルを回すことが必要です。
理解する → 覚える → 使う
解法は、まず「なぜこの手順なのか」を理解します（理屈を知る）。
その上でスムーズに再現するために覚えます（パターン化する）。
そして繰り返し問題を解いて使います（定着させる）。
こうすることで、初めて本番で使える力になります。
NG例 手順だけ丸暗記はキケン！
解法の理屈を飛ばして、手順だけを丸暗記してしまうのは危険です。
よくある失敗例は次のようなパターンです。
★ 全部同じように見える ★
少し問題の設定や図の形が変わっただけで、「暗記したパターン」と違うと感じて手が止まってしまいます。
★ 応用できない ★
応用問題は、いくつかの基本解法を組み合わせたものです。
手順だけを覚えていると、どの解法をいつ使えばいいのか判断できず、手が出なくなります。
丸暗記は一時的な点数にはつながるかもしれませんが、実力が伴わないため、入試本番で通用しにくい勉強法です。
OK例 「自分の言葉」で理解しながら覚える
解法を「使える知識」にするためには、「自分の言葉」で理由を説明できる状態を目指しましょう。
これには、ステップ2で紹介した「再現ノート」が非常に有効です。
★ 自分用の解法ノートの作り方 ★
・【図】：問題の図や条件を図示する。
・【手順】：解法の流れを箇条書きで書く。
・【理由】：なぜその手順を踏むのか（例：なぜここで補助線をひくのか、なぜ図形を分割するのか、なぜ垂線をひいたのか）を、
自分の言葉で簡単に説明する。
★ 暗記カード化・ルール化の例 ★
・表：「問題の条件」 → 裏：「解法ルール」
・例 表：「図形の辺の長さが等しいことを証明する」 → 裏：「その辺を含む合同な図形がないか確認」
※自分なりの言葉でわかりやすくまとめましょう。
このように、問題の型と、それに対する自分の行動ルールを明確にすることで、単なる暗記ではなく、判断力として解法を身につけることができます。
模試・過去問で解法力を試す方法
入試対策の仕上げとなる模試や過去問は、あなたの「解法力」を試す絶好の機会です。
これらの演習は、単に点数を計るためではなく、「どこができなかったか」を見つけて、自分の解法集（定石）に追加していくためのものだと考えましょう。
問題を解き終わった後、わからなかった問題の解説を読んで「次回は再現できるか」までが、過去問演習の重要な復習サイクルです。
5分考えて → 解説 → 再現 が基本サイクル！
過去問や模試を解くとき、
・すぐに諦めないこと
・答えをすぐに確認しないこと
が、解法力を高めるポイントです。
★ まず自力で考える（時間を区切る） ★
問題を前にして手が止まったら、タイマーを使って5分だけ集中して考えましょう。
この5分で「解法のパターン」を思いつけるか試すのが目的です。
★ 時間を区切って解説を確認 ★
5分考えても解法が思いつかなければ、すぐに答えを見るのではなく、「最初のアクション（解法の一歩目）」だけ解説で確認します。
★ 自分で最後まで書き直す（再現） ★
最初の一歩が分かったら、解説を閉じて自分で最後まで解答を書き上げましょう。
この「自分の手で再現する」作業が、解法を定着させます。
このサイクルを回すことで、「思いつかなかった解法」を自分のものにすることができます。
「解けなかった問題」を宝物にする
解けなかった問題は、あなたの弱点ではなく、「次に得点源になる可能性を秘めた宝物」です。
解法を再現できた後、その問題を必ず記録に残しましょう。
・ミスノートや「できなかったカード」に追加
解けなかった問題、あるいは解法を途中で忘れてしまった問題は、ミスノートや暗記カードに追加します。
問題の図や条件と、それに合った解法（最初の一歩）をセットで書き込むことで、「自分専用の解法集」が完成します。
・次回に備える
これらの記録は、試験直前や模試の直前に見直すことで、解法パターンの引き出しを増やす最強の武器となります。
まとめ：今日からできる「解法力UP」3つの行動
今回の記事では、高校受験の数学で点を取るために必要なのは、公式の丸暗記ではなく、
「解法力（定石パターンを使いこなす力）」
であることを解説しました。
数学はセンスではなく、正しい手順でコツコツ積み上げれば必ず伸びる科目です。
難関問題に立ち向かう力をつけるため、今日からすぐに以下の3つの行動を始めましょう。
１．1日1枚、「解法カード」を書く
問題を解いた後、「解き始めの最初の一歩」をカードやノートに記録しましょう。
表： 問題の図や条件（例：問題の図の中に直角三角形がある）
裏： 解法のルール（例：三平方の定理を使って長さを求めることができる！）
毎日少しずつ「定石」をストックしていくことが、解法力を高める一番の近道です。
２．「最初の一手だけ見て」再トライする
もし問題が解き進められなくなったら、すぐに答え全体を見るのはやめましょう。
「解法の最初のアクション（一歩目）」だけ解説で確認し、残りは自力で最後まで解き切る練習をしましょう。
この「自力で再現する」ステップが、あなたの解法を確かな知識に変えます。
３．解けなかった問題を「宝物」としてノートに記録する
模試や過去問で間違えた問題は、あなたの弱点ではなく、「まだ伸びる余地」を示しています。
解法を理解したら、その問題を「自分専用の解法集」としてミスノートに追加しましょう。
入試直前にこれを見直すことが、あなたの点数を確実に上げる最強の復習となります。
高校受験は、解法力をコツコツと積み上げれば、必ず突破できます。
今日から行動を変えて、数学を得点源にしていきましょう！
数学の解法を確認！ 文理のおすすめ問題集
数学の解法を身につけるために役立つ文理の問題集を紹介します。
お客様ひとりひとりのレベルや目的に合わせた教材をご用意しています。
あなたの学習を次のステップに進めるためのおすすめの商品を3シリーズご紹介します。
わからないをわかるにかえる
数学を基礎からじっくり学びたい、どこから手をつけていいかわからなかったという人に最適なシリーズです。
この教材は、「わからない」を「わかる」にかえることを徹底的に追求しています。
定義や公式といった基礎的な内容を、簡単な例題で丁寧に解説しているため、数学が苦手な人でも、着実に基礎から練習を積み重ねることができます。
簡単なステップで自信をつけながら学習を進めたい方に、特におすすめします。
完全攻略
数学の知識を深め、確かな実力をつけたいなら「完全攻略」シリーズが役立ちます。
このシリーズは豊富な演習量が特徴で、基礎の反復から応用までしっかりと問題演習をこなすことで定着させることができます。
また、定期テスト対策ページや、過去の入試問題を扱った実戦問題ページも収録されているため、日々の学習から受験対策まで幅広い学習に対応可能です。
学校の授業の進度に合わせて使いたい方にも最適です。
ハイクラス徹底問題集
難易度の高い問題に挑戦し、数学の応用力をつけたい人向けの最高峰の問題演習集です。
この問題集では、複雑な応用問題や、複数の知識を組み合わせた思考力を要する問題を豊富に扱っています。
難関高校の入試問題も収録されているため、ハイレベルな演習を通じて、ライバルに差をつけたいと考えている学習者を徹底的にサポートします。
現在の学習レベルに関わらず、数学を極めたいという意欲のある方は、ぜひ手に取ってみてください。
関連記事
素数とは？中学数学で押さえておきたいポイント
もくじ 素数って何？基本を知ろう 素数は中学数学でどのように使うの？ 素数を見分ける方法 素数に関するよくある質問 素数の面白い応用例 「わからないをわかるにかえる数学」 「大人の教科書ワーク 数学」 まとめ 素数って何？基本を知ろう 素数の定義をわかりやすく 素数とは、「１とその数自身の積でしか表せない自然数のこと」です。 言い換えると、「１とその数以外に約数ををもたない（約数が２つの）自然数」が素数となります。 ２、３、５、７、・・・ などが素数ですが、例えば７は、１と７でしか割り切れませんから、素数です。 ４や６は、１とその数自身でも割り切れますし、それぞれ２と３でも割り切れますので、素数ではありません。 素数を中学数学で学ぶ理由 素数は、数学の基礎となり、中学数学・高校数学を学ぶうえで必要不可欠な知識となります。 中学では、素数は「素因数分解」や「平方根」で使います。 自然数を素数の積だけで表す素因数分解では、言うまでもなく素数が重要な役割をもっています。 また、小学校５年生で習う「最大公約数・最小公倍数」でも、実は素数が鍵となっています。 数学の基礎となる素数はしっかりと理解を深めておく必要があります。 素数は中学数学でどのように使うの？ 素因数分解で使う例 自然数を素数の積だけで表すことを素因数分解といいます。 素因数分解の基本手順はしたのようになります。 したがって、８４を素因数分解すると、２×２×３×７となります。（実際の問題に答える際には、２²×３×７としましょう。） 最大公約数・最小公倍数の計算での役割 先ほど、最大公約数・最小公倍数で素因数分解が使えると書きましたが、どのように使うのでしょうか。 たとえば、９０と１６２の最大公約数と最小公倍数を考えます。 ９０と１６２をそれぞれ素因数分解すると、こうなります。 これを、下のように縦にそろえて書きます。 ９０と１６２の最大公約数は、したのように考えて、１８だということがわかります。 ９０と１６２の最小公倍数は、したのように考えて、８１０だということがわかります。 このように、最大公約数や最小公倍数を求める際には、素因数分解が役立ちます。 素数を見分ける方法 小さな数で割り算してみる 素数かどうかを見分けるために、小さな数で割り算をしてみるという方法があります。 【手順】 １. まず２で割ってみる 偶数はすべて２で割り切れるので、２以外の偶数は素数ではありません。 例：４、６、８…は２で割り切れるので素数ではない。 ２. 次に３で割る ３で割り切れる場合、その数も素数ではありません。 例：９、１２、１５…は３で割り切れるので素数ではない。 ３. ５で割る 最後の数字が０か５で終わる数は、５で割り切れるため、素数ではありません。 例：１０、１５、２０…は５で割り切れるので素数ではない。 ４. ７、１１、１３、１９…と暗記している素数で割る エラトステネスの篩（ふるい）を使う方法 こちらの方法は、中学数学では習わないのですが、 「エラトステネスのふるい」という名の通り、ふるいにかけるように、多くの数のなかから素数を見つけのに便利です。 この方法を使って、1～40までの範囲の素数を見つけてみましょう。 【手順】 １. １を消す ２. 最も小さい素数を残したまま、その素数の倍数をすべて消す。 この場合は、２を残して、２以外の２の倍数をすべてふるい落とします。 ３. 残っている中で最も小さい素数を残したまま、その素数の倍数をすべて消す この場合は、３を残して、３以外の３の倍数をすべてふるい落とします。 ４. 手順３を最後まで繰り返す。 ４はすべてふるい落とされているので、５を残して、５以外の５の倍数をすべてふるい落とします。 最後まで繰り返すと、下図のようになります。 中学のテストでよく出る素数判定問題 中学のテストでは、ある数が素数かどうかを見分ける問いがよく出題されます。 例えば、 問題：101は素数か答えなさい 解答：101の約数は「１」と「１０１」の２つなので、１０１は素数である。 などです。 上記で紹介した方法などを用いて、素数かどうかを見分けます。 中学では覚えておくべき素数 中学の問題では、少なくとも【２,３,５,７,１１,１３,１７,１９】あたりまでの素数を暗記しておくとよいでしょう。 暗記をしておくことで、素数を見分ける問題が楽に解けるようになります。 もちろん、素数はずっと続いていきますので、興味があれば暗記してみても面白いかもしれないですね。 素数に関するよくある質問 ・１は素数じゃないの？ 素数の定義をみてみると、「１とその数以外に約数ををもたない（約数が２つの）自然数」となっています。 たとえば、２の約数は１と２の２つ、７の約数は１と７の２つ。 １は、約数が１自身の１つだけしかないので、素数ではないということになります。 ・なぜ2は素数なのか？ なんとなく、２は偶数だから素数ではない気がしてしまいますが、２は素数です。 ２は、「１」と「２」自身の２つの約数をもつ自然数なので、２は素数となります。 うっかりミスで、２が素数ではないと勘違いしないようにしましょう。 ・素数は無限にあるの？ 素数は無限に存在します。 素数が無数に存在することの証明は、色々な方法でされています。 有名なのは、背理法によるユークリッドの証明です。こちらは紀元前に発見されたものです。 そのほかにも、フェルマー数を用いたゴールドバッハの証明や、2006年に発表されたサイダックの証明などがあります。 ・素数は何年生で学ぶ？ 素数は、中学１年生で学びます。 現行の学習指導要領では、素数を１年において扱うことにより、 素因数分解を自然数、素数、倍数、約数、公倍数、公約数などと関連づけ、 整数の性質を探るひとつの道具として利用することができるとしています。 参考：文部科学省「中学校学習指導要領(平成29年告示)解説」2017年 ▼文部科学省ホームページ 中学校学習指導要領解説：文部科学省 ・100までの素数リストは？ １～１００までに、素数は 「 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97」があり、全部で25個あります。 下図の白い背景のマスが、素数です。 素数の面白い応用例 素数は、とても不思議な数字です。 身近でも、素数の面白い応用例や、素数に絡んだ不思議なことがたくさんあります。 インターネットの暗号に使われる素数 インターネット上の情報を守るのに「暗号化」という技術が使われていますが、この暗号化において素数が重要な役割を担っています。 とある文書があったとき、素数×素数のかけ算で文書に暗号をかけます。 第三者には、かけ算の結果が公開されています。 暗号を元の文書に戻すためには別の鍵が必要です。 この鍵を得るためには、自然数＝素数×素数と、逆の計算をしなければいけません。 地道に計算するので、素数の桁が大きいほど大変です。 簡単な例で考えると、１９×２３のかけ算はひっ算を使えばすぐできるけど、437＝19×23を逆の計算をするのは大変ですよね。 この作業は、コンピューターでも膨大な時間がかかるため、インターネットのセキュリティでは素数が重要な役割を担っているということです。 自然界の不思議：セミと素数の関係 素数ゼミとよばれるセミを聞いたことがあるでしょうか。 素数ゼミとは、生き残り戦略のために、１３年、もしくは１７年の間、地中にいるセミのことです。 それでは、なぜ素数である１３年、もしくは１７年の間、地中にいることが生き残り戦略となるのでしょうか。 その秘密は、最小公倍数にあります。 例えば、１３年ゼミ周期で土の中から出てくる素数ゼミに、３年周期で発生する天敵がいたとします。 天敵が３年周期で発生していても、同じ年に１３年周期ゼミが地上に出るのは、上の表のように３９年経ったときのみです。 ３９は、１３と３の最小公倍数です。１３が素数であるため、３を約数に持たないことから、この最小公倍数が大きくなっています。 仮にセミの地上にいる期間が１年短い１２年だとすると、地上に出れば毎回３年周期で発生している天敵がいるということになってしまいます。 セミの発生周期が素数であることは、その数自身しか約数がない自然数である素数を地上にでる周期にすることで、 天敵とできるだけ出会わないようにする、セミの生き残り戦略と考えることができます。 「わからないをわかるにかえる数学」 ここでPR！ 今回解説した「素数」は中学１年生で学びます。 そんな中学生向けの中学生向けの超基礎シリーズが、こちらの『わからないをわかるにかえる』。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▶シリーズページはこちら ▶ご購入はこちら 「わからないをわかるにかえる高校入試数学」 人気の超基礎シリーズ「わからないをわかるにかえる」の高校入試対策版です。 中学3年間の内容を基礎からおさらいできます。 やさしい言葉遣いやイラストで、とっつきやすいのが特徴で、苦手な分野が多く、易しめから入りたい人はチェックしてみてください。 ▶シリーズページはこちら ▶ご購入はこちら 「大人の教科書ワーク 数学」 日常の悩みや疑問を、小中学校の教科書で解決！ それがこちらの『大人の教科書ワーク』です。 実は、今回の記事のなかで紹介した「インターネットの暗号に使われる素数」や「セミと素数の関係」について、 この『大人の教科書ワーク数学』ではさらに詳しく書かれています！ この本では、このような数学にまつわる面白いトピックをたくさんとりあげています。 「大人の学び直し」がテーマの本ですが、小中学校の教科書で習う算数・数学の内容を用いながら、 日常のあらゆる疑問に答える形式になっているので、いままさに数学を学んでいる中学生が数学を学ぶ楽しさを知るのにもぴったりです！ ▶シリーズページはこちら ▶ご購入はこちら まとめ いかかでしたか。 今回の記事では、素数の定義から中学数学で押さえておきたいポイント、素数を応用した例までご紹介しました。 素数は数学の基礎であると同時に、どこか不思議な数字ですよね。 素数を通じて数学の魅力に触れ、ぜひ今の学びを深めてみてください！
小学生でもわかる！パーセント計算のやり方とコツ
もくじ はじめに パーセントとは？ パーセント計算の基本ルール 割引や増加・減少とパーセント計算 パーセントの計算をもっと楽しくするコツ 計算が得意になる！ おすすめ問題集 まとめ はじめに 「この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は…」 「水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何％かな？」 「この服、4500円だけど30%オフになっているよ！いくらになるのかな？」 私たちの生活の中には、パーセント(%)という言葉がたくさん出てきます。 パーセントを理解すると、身の回りのことがよくわかるようになります。 この記事では、小学生のみなさんにもわかりやすいように、パーセントの基本的な考え方、計算方法、ちょっとしたコツなどを紹介します。 パーセントの世界を一緒に探検してみましょう！ パーセントの計算ができる文理のドリルシリーズはこちら！ できる!!がふえる↑ドリル ハイレベル算数ドリル 小学教科書ドリル パーセントとは？ ◆パーセントの意味 普段の生活の中でパーセント(%)という記号をよく見かけますよね。 これは、 「全体を100としたときにどのくらいあるか」 を表す記号です。 「％」を使って表す割合を、百分率といいます。 全体を100(百)としているので百分率です。 たとえば、全体で100人いる中で、20人がめがねをかけているとき、めがねをかけている人は「20%」になります。 全体を100として考えることで、全体の数が半端な数であっても、どのくらいあるかわかりやすくなります。 ◆割合、歩合、百分率の関係 百分率と合わせて、割合や歩合という言葉も使われます。 これは、全体を何にするかで使い分けます。 ・割合 → 全体を1としたときにどのくらいあるか。 単位はつけません。 ・歩合 → 全体を10としたときにどのくらいあるか。 単位は割(わり)、分(ぶ)、厘(りん)などを使います。 ・百分率 → 全体を100としたときにどのくらいあるか。 単位は％です。 割合を10倍すると歩合、割合を100倍すると百分率になります。 具体例で確認してみましょう。 全体で100人いる中で、20人がめがねをかけているとき、 ・割合 → 0.2 (20÷100=0.2) ・歩合 → 2割 (20÷100×10=2) ・百分率 → 20% (20÷100×100=20) となります。 ３つの関係を表にまとめると、関係がわかりやすくなります。 歩合が使われることは減っていますが、野球の打率を表すときに使われます。 例：文理野球部４番バッターの今年の打率は、3割ちょうどでした。 この場合、このバッターは、10打席中３打席ヒットやホームランを打つと考えられます。 パーセント計算の基本ルール ◆「○○の□□％」を計算する方法 ここからは、テストでもよく出る問題の解き方を、パターン別に解説します。 解き方を確認したら、練習問題にもチャレンジしてみましょう！ 例題 400円の20％は？ 解き方・答え 計算するときは、百分率を割合に直します。 20% → 0.2 (20÷100=0.2) 400×0.2＝80(円) 20のまま計算しないよう注意しましょう。 では、練習問題です！ 練習問題 ★次の計算をしましょう。 １．800gの20％は？ ２．600Lの30％は？ ３．700人の15％は？ ４．この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は… ↑４は、はじめにで紹介した問題です！ 解き方・答え １．20% → 0.2 800×0.2=160(g) ２．30% → 0.3 600×0.3=180(L) ３．15% → 0.15 700×0.15=105(人) ４．10% → 0.1 500×0.1=50(ｍL) パーセントを使って計算するときは、百分率を割合に直すことを忘れないようにしましょう。 ◆「□□は○○の何％？」を計算する方法 次は、割合を計算してからパーセントを求める問題です。 例題 80円は400円の何％？ 解き方・答え まず、割合を求めます。 80÷400=0.2 何％か求めるので、100をかけて百分率に直しましょう。 0.2×100=20(%) では、練習してみましょう！ 練習問題 ★次の計算をしましょう。 １．50gは200gの何％？ ２．48Lは80Lの何％？ ３．150人は1250人の何％？ ４．水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何％かな？ 解き方・答え １．50÷200=0.25 0.25×100=25(%) ２．48÷80=0.6 0.6×100=60(%) ３．150÷1250=0.12 0.12×100=12(%) ４．6÷300=0.02 0.02×100=2(%) 百分率(パーセント)で答えるので、100をかけて百分率に直すことに注意しましょう。 割引や増加・減少とパーセント計算 ◆割引とパーセント お店で買い物をするときに、「30%オフ！」というPOPを見かけることはありませんか？ これは、元の値段から30%安くなることを表しています。 割引されるときのパーセントの計算を確認しましょう！ 例題 5000円の服が40%オフで売られています。支払う金額はいくらですか？ 解き方・答え 40%が0.4であることに注意して、まずは安くなる金額を求めます。 5000×0.4=2000(円) 次に、支払う金額を求めます。 5000-2000=3000(円) では、練習してみましょう。 練習問題 ★次の問題に答えましょう。 １．800円のお菓子が15%オフで売られています。支払う金額はいくらですか？ ２．2500円の商品が20%オフになっています。支払う金額はいくらですか？ ３．定価12000円の自転車が35%オフで売られています。支払う金額はいくらですか？ ４．この服、4500円だけど30%オフになっているよ！いくらになるのかな？ 解き方・答え １．800×0.15=120(円) 800-120=680(円) ２．2500×0.2=500(円) 2500-500=2000(円) ３．12000×0.35=4200(円) 12000-4200=7800(円) ４．4500×0.3=1350(円) 4500-1350=3150(円) ◆増える・減るときのパーセント 増えたり減ったりするときにもパーセントは使われます。 例題 タケルさんの今回のテストの点数は、前のテストの点の80点より15%増えました。 今回のテストは何点でしたか？ 解き方・答え まず、増えた点数を求めます。 80×0.15=12(点) 次に、今回の点数を求めます。 80+12=92(点) では、練習問題です！ 練習問題 ★次の問題に答えましょう。 １．ユイさんの身長は、１年前に150cmでしたが、この1年で5%伸びました。今の身長は何cmですか？ ２．A地域の人口は、昨年10000人でしたが、今年は2%減りました。A地域の今年の人口は何人ですか？ ３．お父さんの体重は60kgでしたが、ダイエットをして10%減らしました。ダイエット後の体重は何kgですか？ 解き方・答え １．150×0.05=7.5(cm) 150+7.5=157.5(cm) ２．10000×0.02=200(人) 10000-200=9800(人) ３．60×0.1=6(kg) 60-6=54(kg) より多くの問題を解きたい方はこちら！ できるが!!ふえる↑ドリル ハイレベル算数ドリル 小学教科書ドリル パーセントの計算をもっと楽しくするコツ ◆暗算のちょっとしたテクニック ここからは、知っていると便利なテクニックを紹介します。 よく出るパーセントの計算方法を覚えておくと、暗算で答えが出せるようになることがあります。 ・10% → 元の数を10でわるのと同じ！ 例：290円の10%は？ 290÷10=29(円) ・50% → 元の数を2でわるのと同じ！ (元の数の半分！) 例：800個の50%は？ 800÷2=400(個) ・25% → 元の数を4でわるのと同じ！ (元の数の4分の1！) 例：200ページの25%は？ 200÷4=50(ページ) ・20% → 元の数を5でわるのと同じ！ 例：500mLの20%は？ 500÷5=100(mL) これらのテクニックを覚えておくと、暗算できることがあります。 ◆クイズでパーセントをマスターしよう！ ここまで学習してきたパーセントの計算を使って、クイズに答えてみましょう。 問題 ★次の問題に答えましょう。 １．定価1000円のものが60%オフで売られています。 財布に500円しかないとき、この商品を買える？買えない？ ２．50点満点のテストの結果が40点でした。90%正解したことになる？ ３．果汁20%の飲み物を２本買って混ぜたら、果汁は40%になる？ ４．450円の80％と、700円の50％では、どちらが安い？ 解き方・答え １．1000×0.6=600(円) 1000-600=400(円) 500円あるので買えます。 答え 買える。 ２．40÷50=0.8 0.8 → 80% 答え 90%正解したことにはならない。 ３．果汁20%の飲み物を何本混ぜても、果汁は20%のままです。 答え 果汁40%にはならない。 ４．450×0.8=360(円) 700×0.5=350(円) 答え 700円の50％の方が安い。 計算が得意になる！ おすすめ問題集 文理の書籍には、計算練習ができるものがたくさんありますので紹介します。 今回紹介したパーセントの計算以外の計算問題もたくさんあります。 計算力をつけるには問題をたくさん解くことが一番！ 力をつけたい方はぜひチャレンジしてみてください。 ※パーセントの問題は、小学5年生で詳しく学習します。 パーセントの問題を練習したい方は、小学５年生の書籍をご利用ください。 ◆小学教科書ワーク 「算数」 教科書に完全対応しているから、学校の授業に合わせて使いやすい！ 計算練習ノート、ポスター、動画、CBTなど付属品も充実！ 全教科書に対応した「数と計算」「文章題・図形」シリーズも用意しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆小学教科書ドリル 「算数」 1回10分で終わるドリルだから、習い事など忙しくても続けやすい！ 基本・確認の２ステップで、無理なく力がつきます！ 計算問題に特化した「計算編」文章題や図形問題に特化した「文章題、数・量・図形」シリーズも用意しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆できる!!ふえる↑ドリル １枚ずつはがして使えるから、学習しやすい！ 「計算」「文章題」「数・量・図形」「時こくと時間」など、分野別のシリーズが充実しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆ハイレベル算数ドリル 3段階構成で取り組みやすい！ 詳しい回答解説で、学習をサポート！ ▶シリーズページはこちら ▶ご購入はこちら まとめ 今回の記事では、パーセントの基本的な意味から、計算の仕方、そしてちょっとしたコツまでを解説してきました。 パーセントは、私たちの身の回りの色々なところで使われています。 色々な問題にチャレンジして、パーセントマスターを目指してくださいね！
中学数学の公式をわかりやすくまとめます！高校入試にも役立つ完全ガイド
もくじ はじめに 中学数学で覚えるべき公式とは？ 高校入試で役立つ公式 「なぜそうなるか」から数学公式を理解する 覚え方・使いこなし練習 おすすめの学習教材 まとめ はじめに 「数学の公式って、たくさんあって覚えきれないな…」 「高校入試に向けて、どの公式をしっかり押さえておけばいいんだろう？」 そんな悩みを解消するために、今回は中学数学で学ぶ公式を解説します！ 公式を「知る」から「使える」に変えるための完全ガイド、ぜひ最後まで読んでみてくださいね！ 中学数学で覚えるべき公式とは？ 中学3年間で学習する数学は、主に計算（方程式）、関数、図形の3つの分野に分類できます。 ※データの活用もありますが、今回は公式ということで省略します。 一見するとバラバラに見えるかもしれませんが、実はどれも深いところでつながっています。 学年ごとに確認しましょう。 中1で習う数学公式のポイント 中学1年生になると、算数から数学に教科名が変更され、本格的な数学の学習が始まります。 中学1年生で学習する公式は、この先の数学の土台になりますのでしっかり理解しましょう。 ◆ 正の数・負の数【計算】 四則演算（たし算、ひき算、かけ算、わり算）は、符号ミスに注意することが大切です。 符号の関係を公式としてまとめておくと便利です。 ◆ 文字式【計算】 分配法則は、今後の計算の基本になりますのでここで理解しておきましょう。 割合や速さの関係も、文章題を解く上で大切です。こちらは小学校での学習内容になりますが押さえておきましょう。 ◆ １次方程式【計算】 等式の性質が方程式を解くときの基本になります。移項するときは符号に注意しましょう。 ◆ 比例・反比例【関数】 関係式を公式として整理しましょう。座標の読み取り方も重要です。 ◆ 平面図形・空間図形【図形】 おうぎ形の面積、立体の体積を公式として覚えておきましょう。 おうぎ形は円の一部分だとイメージすると、計算するときに式を思い出しやすくなります。 中2で習う数学公式のポイント 中学2年生では、さらに一歩進んだ内容を学習します。 図形の単元で証明を学習し、ものごとを順序だてて説明する力を養います。 図形に関する公式（定義や定理）が増えますので、正確に理解する力が求められます。 ◆ １次関数【関数】 y=ax+b の形と式の意味、変化の割合などを覚えましょう。高校入試や定期テストでは、図形問題に応用されることも多いです。 ◆ 平行と合同【図形】 平行線と角の関係や、多角形の内角の和・外角の和は、入試の図形問題を解く際にも重要な内容です。 三角形の合同条件は、証明問題を解く際、数多く出てきます。 ◆ 特別な四角形【図形】 平行四辺形、長方形、ひし形、正方形の定義や性質は、小学校で学習した内容でもあります。 中学２年生では、定義、定理として再確認します。 中3で習う数学公式のポイント 中学3年生で学習する公式は、高校入試に直結する重要なものが多くあります。 特に平方根、２次方程式、相似、円、三平方の定理は、入試の頻出単元として強調しておきたいポイントです。 ◆ 多項式【計算】 展開や乗法公式、因数分解の公式が出てきます。因数分解は、２次方程式を解くときにも役立ちます。 ◆ 平方根【計算】 無理数（分数で表すことのできない数）へと数の世界が広がる面白い単元です。 新しい記号であるルートの計算方法を、公式として押さえておきましょう。 ◆ ２次方程式【計算】 主に３つの解き方があります。 因数分解を利用した解き方、解の公式を覚えておくと安心です。 ◆ 相似【図形】 三角形の相似条件は、合同条件との違いを意識して覚えましょう。 線分の比の関係、面積比、体積比は、入試でよく問われます。 ◆ 円【図形】 円や弧を見つけたら、円周角の定理を意識しましょう。 半円の弧に対する円周角が直角(90°)であることも覚えておくと便利です。 ◆ 三平方の定理【図形】 直角三角形の辺の長さの関係を表す定理です。 高校入試頻出で、関数もふくめ、多くの問題で応用されます。 高校入試で役立つ公式 高校入試でよく出る公式を厳選しました。 これらを重点的にマスターし、入試本番で得点アップを目指しましょう。 入試でよく出題される公式には理由があります。 それは、単に知識を問うだけでなく、複雑な問題を解く際に利用したり、他の単元にも応用できるからです。 それでは順番に見ていきましょう。 1. 三平方の定理 図形問題で辺の長さを求めるときに必須です。 平面図形だけでなく、関数や空間図形にも応用されます。 長さを求める問題が出てきたときは、三平方の定理が使えないか意識しましょう。 図形の中にひそむ直角三角形を見つけることがポイントです。 2. ２次方程式の解の公式 因数分解を利用して解けない方程式でも解ける万能な公式です。 因数分解が思いつかなくても焦らなくなります。 3. 関数とグラフの式 直線の式（１次関数の式） y=ax+b 放物線の式 y=ax2 双曲線 y= x a グラフから式や座標を求める問題は頻出です。 グラフの特長と式の形を整理しておきましょう。 比例y=axのグラフは原点を通る直線ですので、１次関数でb=0のときと覚えておくと便利です。 4. 展開・因数分解の公式 単問の計算問題だけでなく、文章題で式をつくった後の計算で利用することもあります。 ２次方程式を解く際にも役立ちます。 5. 合同条件・相似条件 図形の証明問題で必須です。減点対象にもなるので、正確に書けるように覚えましょう。 辺の長さを求めるときに、図形が合同、相似であることを利用する場合もあります。 6. 円周角の定理 円に関する図形問題で、角度を求めるときによく使われます。 図形の中に円や弧を見つけたら、円周角の定理を意識して角度を調べてみましょう。 7. 多角形の内角の和・外角の和 基本的な図形問題や証明問題で使われます。 どんな多角形でも外角の和は360°ですので、外角から考えると計算しやすくなる場合もあります。 入試での使われ方と注意点 高校入試では、公式をただ覚えているだけでは点数につながりません。 公式が「どんなパターンで出題されるか」を知り、「使いこなす力」を身につけることが何よりも重要です。 例えば、三平方の定理は、関数や空間図形の中に隠れていることもあります。 公式を使えるようになるために、様々な問題を解くことが何よりも大切です。 また、一つの問題で複数の公式を組み合わせるパターンもよく出題されます。 公式を単独で覚えるだけでなく、それぞれの公式がどう連携し合っているのか、全体像を意識して学習に取り組みましょう。 「なぜそうなるか」から数学公式を理解する 公式を丸暗記するだけでは、少し問題がひねられると対応できなくなってしまいます。 公式が「なぜそうなるのか」、その成り立ちを理解することで、忘れにくく、応用も効く「使える知識」になります。 • ２次方程式の解の公式 なぜあの複雑な形になるのか？ これは平方完成という考え方から導き出されます。 式の変形を順を追って理解することで、公式がより深く頭に残ります。 • 三平方の定理 なぜ a2+b2=c2 なのか？ これは、直角三角形の各辺を一辺とする正方形の面積の関係を表しています。 図を使って考えることで、視覚的に理解を深められます。 • 円周角の定理 なぜ「中心角の半分になる」のか？ これは補助線をひいて、二等辺三角形の性質を使うと、簡単に証明できます。 このように、「なぜ？」という疑問を持つことは、数学の面白さを発見する第一歩です。 公式を使って問題をたくさん解くとともに、その公式がなぜ成り立つのか調べてみると理解が深まります。 覚え方・使いこなし練習 公式を覚えるには、ただ眺めているだけでは不十分です。 効果的な覚え方と、実際に使いこなすための練習法を知ることが、記憶定着と応用力アップのカギとなります。 語呂合わせ・図解を活用しよう 文字ばかりの公式を覚えるのが苦手なら、語呂合わせや図解を積極的に活用しましょう。 例えば、球の表面積や体積の公式などは語呂合わせがあります。 ・球の表面積は、「心配（4π）あるある（r2）」 ・球の体積は、「身の上に心配（ 4π 3 ）あるから参上（r3）」 公式を覚えるときに、自分だけの語呂合わせをつくってみましょう。 友達と共有しても面白いかもしれません。 円周角の定理などは、図で視覚的に理解する方が記憶に残りやすいです。 図解が必要な公式は、自分で簡単な絵をかいたり、教科書や参考書の図をじっくり見たりして、「なぜこうなっているんだろう？」と考えてみましょう。 視覚を利用して覚えることで、いざという時に「あの図だ！」と思い出しやすくなります。 公式を使う練習のすすめ 公式は、問題演習とセットで覚えることが記憶定着のコツです。 覚えた公式を、実際に問題を解きながら使ってみることで、その使い方や、どんな時に使うべきかが自然と身につきます。 間違えた問題は、なぜ間違えたのか、どの公式の使い方が間違っていたのかをしっかり確認し、もう一度解き直しましょう。 この繰り返しが、公式を「使える力」に変える最も効果的な方法です。 おすすめの学習教材 公式の理解と定着を深めるためには、適切な教材選びも重要です。 ここで、皆さんの学習を強力にサポートしてくれる教材をご紹介します。 ◆ 中学教科書ワーク 学校の教科書の内容に沿ってつくられているため、日々の授業の予習・復習に最適です。 イラストや図解が豊富で、数学の公式も詳しく解説されています。 高校入試に有効な問題も多くふくまれており、基礎から応用まで着実に力をつけることができます。 ▶シリーズページはこちら ▶ご購入はこちら ◆ わからないをわかるにかえる ニガテなところがどんどんわかる！超基礎からやさしく学べる、中学生のための問題集！ 数学の基本的な問題の解き方を丁寧に解説しています。 公式も覚えやすくなるよう配慮していますので、数学が苦手な方でも大丈夫。 小学生の先取り学習や、高校生・大人の学び直しにもおすすめです。 学年別・領域別と、高校入試シリーズがあります。 ▶シリーズページはこちら ▶ご購入はこちら ◆ 完全攻略 教科書だけではもの足りないキミに送る、定期テスト対策から高校入試の基礎固めに最適な問題集です。 ▶シリーズページはこちら ▶ご購入はこちら ◆ ハイクラス徹底問題集 最高峰の問題演習で、「試験に強い実力」をつけられる問題集です。レベルの高い問題にチャレンジしたい方に最適です。 ▶シリーズページはこちら ▶ご購入はこちら まとめ 公式を「使える力」に変えよう ここまで、中学数学の公式について、その種類から高校入試での重要性、そして効果的な学習法まで、幅広く紹介してきました。 大切なのは、公式を「知る」→「理解する」→「使えるようになる」という段階をしっかり踏むことです。 丸暗記ではなく、「なぜそうなるのか」を考え、実際に問題を解きながら使いこなす練習を続けましょう。 それが、数学の力を大きく伸ばすカギとなります。 紹介した文理の教材をうまく活用し、公式を「使える力」に変えて、自信を持って高校入試に挑んでくださいね。 皆さんの学習がより充実したものになるよう、心から応援しています！
【中学生向け】因数分解のやり方と公式一覧 テストで使えるコツも解説
もくじ はじめに 因数分解とは？ 因数分解の解き方：共通因数でくくる 因数分解の解き方：４つの公式 因数分解の解き方ステップ 練習問題で確認しよう まとめと商品紹介 はじめに 今回のテーマは中学3年生の数学で出てくる「因数分解」です。 「因数分解」という言葉を聞いて、 「難しそう…」 「公式がたくさんあって覚えられない！」 と感じている人もいるかもしれません。 しかし、心配はいりません！ 因数分解は、中学数学の大きな柱ですが、正しい手順といくつかのコツさえつかめば、必ず理解できるようになります！ この記事では、因数分解が「なぜ大切なのか」という基礎から、テストで使える4つの公式、さらには応用問題の解き方まで、ステップごとにわかりやすく解説します。 この記事を最後まで読んで、因数分解への理解を深め、定期テストや高校入試で自信を持って問題が解けるようになりましょう！ 因数分解とは？ 因数分解とは、簡単に言うと「多項式をかけ算の形（因数の積の形）になおす操作」のことです。 まずは因数について確認しましょう。 例えば、6という数は、次のようにかけ算の形になおすことができますね。 6=2×3 このとき、2や3を6の因数と呼びます。 因数分解とは、多項式をいくつかの因数の積の形に分解することです。 【例】 2a2+6ab=2a(a+3b) 左側の式 2a2+6ab はたし算（単項式の和）の形ですが、 右側の式 2a(a+3b) は、2 と a と (a + 3b) という因数のかけ算の形になっています。 展開と因数分解の関係 因数分解を理解する上で、展開（てんかい）との関係を知っておくことが大切です。 因数分解は、展開の逆の操作だと考えると、イメージがしやすいでしょう。 展開：かけ算を計算して、たし算・ひき算の形になおすこと (x+2)(x+3) ― 展開 → x2+5x+6 因数分解：たし算・ひき算の形を、かけ算の形になおすこと x2+5x+6 ― 因数分解 → (x+2)(x+3) このように、展開と因数分解は、「たし算・ひき算の形」と「かけ算の形」を行き来する、裏表の関係になっています。 このイメージを持っておくと、公式を理解する際にも役立ちます。 なぜ因数分解を学ぶのか 「わざわざ式をかけ算の形になおすのはなぜ？」 と思うかもしれません。 ここでは、因数分解を学ぶ理由を3つ紹介します。 • 2次方程式を解くため x2+5x+6=0 のような2次方程式の解を求めるときは、左辺を因数分解をして、 (x+2)(x+3)=0 の形になおすことで、 x=−2 または x=−3 という解を求めることができます。 • 計算を簡単にするため 複雑な多項式を因数分解してシンプルな形にすることで、計算ミスを防ぐことにつながります。 特に、「式の値」を求めるときに役立ちます。 【例】 x=98のとき、x2+4x+4 の値を求めましょう。 直接代入して求めることもできますが、 982+4×98+4 を計算するのはたいへんです。 そこで、先に因数分解をして (x+2)2 にしてから代入します。 (98+2)2 = 1002 = 10000 と、計算が簡単になります！ • 高校数学の基礎となるため 高校で学ぶより高度な数学（数Ⅱ、数Bなど）でも、因数分解は当たり前の基礎技術として使われます。 今のうちにしっかり身につけておくことが、将来の数学の土台となります。 因数分解は、定期テストでも高校入試でも必ず頻出する重要な分野です。 しっかり理解を深め、数学の基礎力を身につけましょう！ 因数分解の解き方：共通因数でくくる ここからは、因数分解の解き方についてです。 因数分解をするとき、まず最初に考えるべきなのが、「共通因数でくくる」という方法です。 共通因数でくくるとは？ 共通因数とは、多項式のすべての項に共通してかけられている数や文字のことです。 多項式を、共通因数と残りの部分の積の形になおす操作を、「共通因数でくくる」「共通因数でくくり出す」と言います。 これは、展開のときの分配法則の逆の操作です。 【例】 2x+6 を因数分解しましょう。 １．共通因数を見つける それぞれの項 ( 2x と 6 ) の中に共通して含まれている因数を探します。 2x=2×x 6=2×3 両方の項に共通しているのは、2 です。 つまり、共通因数は 2 です。 ２．共通因数でくくる 共通因数 2 を式の前に出し、かっこでくくります。 2x+6=2(x+3) 符号と文字の扱いに注意する 多項式の最初の項がマイナスのときは、マイナスも共通因数の一部としてくくり出すことが多いです。 特に、共通因数に文字も含まれる場合は注意が必要です。 【例】 −3ab+12bを因数分解しましょう。 この式は、共通因数として数(係数)と文字の両方に着目します。 １．共通因数を見つける 数(係数)の部分 ： −3 と +12 の共通因数は −3 文字の部分 ： ab と b の共通因数は b です。 したがって、共通因数は −3b です。 ２．共通因数でくくる −3ab+12b=−3b(a−4) 【注意】 マイナスでくくると、かっこの中の項の符号がすべて逆になることに注意しましょう。 ○ −3ab+12b=−3b(a−4) × −3ab+12b=−3b(a＋4) 因数分解の解き方：４つの公式 共通因数でくくれない場合、次に因数分解の4つの公式を使います。 これらは、展開の公式を逆にしたものです。 展開の公式をしっかり覚えていると、スムーズに理解できます。 公式① x²+(a+b)x+ab=(x+a)(x+b) これは「たして (a+b)、かけて ab」になる a と b の組み合わせを見つける公式です。 【式の形】 x の項の係数が a+b(和）、定数項が ab(積）になっているのが特徴です。 【解き方のコツ】 １．まず、定数項 ab に注目し、積になる a と b のペアを考えます。 ２．そのペアの中で、和が x の項の係数 (a+b) になるものを見つけます。 ３．見つけた a と b を (x+a)(x+b) の形に当てはめます。 【例】 x2+7x+12 を因数分解しましょう。 １．積が 12 になるペアを探します。 (1, 12)、(2, 6)、(3, 4) … ２．その中で、和が 7 になるペアはを見つけます。 (3, 4) ３．x2+7x+12=(x+3)(x+4) 公式② x²+2ax+a²=(x+a)² 公式③ x²－2ax+a²=(x－a)² これらは、「和の平方」「差の平方」と呼ばれる公式です。 公式①で、 a=b の特殊なパターンと考えると理解しやすいでしょう。 【式の形】 xの項の係数が 2a ( a の2倍)、定数項が a2 ( a の2乗) になっているのが特徴です。 （※公式③は符号がマイナスです。） 【解き方のコツ】 １．定数項が、ある数 a の2乗になっていることを確認します。 ２． x の項の係数が、1で確認したaの2倍になっているかを確認します。 ３．符号に注意して (x±a)2 の形になおします。 【例】 x2−10x+25 を因数分解しましょう。 １．定数項 25 は 52 、または (−5)2 です。 ２．xの項の係数 −10 は、−5 の 2 倍なので、公式③で a=5 のときだとわかります。 ３．x2−10x+25=(x−5)2 公式④ x²−a²=(x+a)(x－a) (2乗)ー(2乗) の形をした因数分解の公式です。 公式①で、 b=ーa の特殊なパターンと考えると理解しやすいでしょう。 【式の形】 x の項の係数が 0 になっていて、項が2つしかないのが大きな特徴です。 【解き方のコツ】 １．式が (2乗)ー(2乗) の形になっているかを確認します。 ２．(x+a)(x−a) の形に当てはめます。 【例】 x2−49 を因数分解しましょう。 １． 49 は 72 なので、x2− 72 の形です。 ２．x2−49=(x+7)(x-7) 展開公式との関係 公式①から④は、すべて展開公式を逆にしたものです。 因数分解ができたら、展開し直して元の式に戻るか確認する習慣をつけましょう。 これにより、ミスが減り、公式の理解もさらに深まります。 x2+7x+12 ― 因数分解 → (x+3)(x+4) (x+3)(x+4) ― 展開 → x2+7x+12 因数分解の解き方ステップ これまでに学んだ「共通因数でくくる」方法と「4つの公式」を使えば、多項式の因数分解ができるようになります。 しかし、問題を見たときにどの方法を使えばいいか迷ってしまうことがありますよね。 ここでは、因数分解のときに迷わず正解にたどり着くためのステップを解説します。 １．共通因数を探す 因数分解を始めるとき、公式が使えるかどうかを確認する前に、必ず共通因数があるかを確認しましょう。 共通因数を見つけてくくり出すことで、その後に使う公式を見つけやすくなります。 【チェックポイント】 すべての項に共通する因数（数や文字）はないか？ 【注意点】 共通因数をくくり出すのを忘れると、完全に因数分解された形にたどり着けなくなります。 ２．使える公式があるか判断する 共通因数をくくりだしたあと、残った多項式を見て、どの公式が使えるかを判断します。 次のように順序だてて考えましょう。 【項が２つ】 → 公式④ x²−a²=(x+a)(x－a) が使えるか確認する 【項が３つ】 → 【定数項が a² の形になっている】 → 公式② x²+2ax+a²=(x+a)² 公式③ x²－2ax+a²=(x－a)² が使えるか確認する → 【定数項が a² の形になっていない】 → 公式① x²+(a+b)x+ab=(x+a)(x+b) が使えるか確認する 工夫して分解する応用パターン 共通因数やくくり出し、公式を組み合わせることで解ける応用問題のパターンをいくつかご紹介します。 「これ以上分解できない」状態まで分解しきるのが因数分解のゴールです。 １．複雑な式は展開してから分解する 元の式が複雑なかっこのかけ算の形になっている場合、まずは展開して同類項をまとめることで、公式が使える形になることがあります。 【例】 (x+3)(x−1)−12 ← 展開の公式を使って展開します =x²+2x−3−12 ← 同類項をまとめます =x²+2x−15 ← たして +2、かけて -15 になる数（5，－3）を探して、公式①を使います =(x+5)(x−3) ２．多項式を共通因数としてくくり出す 共通因数が数や文字ではなく、多項式になる場合もあります。 多項式全体を１つのかたまりと考えて、共通因数をくくり出します。 一見共通因数がないように見えても、一部を因数分解すると共通因数が見つかることがあります。 【例】 5(a−2)+a²−2a ← 5(a−2) と a²−2a に分けて考え、後ろの式で a をくくり出します =5(a−2)+a(a−2) ← 多項式 (a−2) が共通因数になっているので、くくり出します =(a−2)(5+a) ３．共通因数をくくり出してから公式を使う 共通因数でくくり出したあと、さらに因数分解できる場合があります。 因数分解できるかどうか、必ず最後までチェックしましょう。 【例】 3x³y−12xy³ ← 共通因数 3xy でくくり出します =3xy(x²−4y²) ← x²−4y² で、公式④を使って因数分解します =3xy(x+2y)(x－2y) ４．x² の項の係数が1でない式 x² の項の係数が常に1とは限りません。 そんな式でも、公式②または③が使える場合があります。 何かの2乗になっているか考えるのがポイントです。 【例】 9x²−6xy+y² ← 公式が使える形に変形します =(3x)²−2×3x×y+y² ← 公式③を使います =(3x−y)² 練習問題で確認しよう これまでの知識が定着しているか、以下の問題で確認してみましょう。 因数分解は、「共通因数」→「公式」の順番で考えることが大切です！ 【問題】 次の式を因数分解しましょう。 １．4x²−16x ２．a²+8a+15 ３．25x²−16y² ４．3x²−30x+75 ５．(x+3)²−5(x+3) 【ヒント】 解き方に迷ったら、以下のヒントを参考にしてください。 １．まずは、数と文字の共通因数を見つけて、くくり出しましょう。 ２．公式①のパターンです。たして +8、かけて +15 になる2つの数を探しましょう。 ３．(2乗)ー(2乗) の形です。公式④を使いましょう。 ４．最初に共通因数の3をくくり出し、かっこの中の式で公式③を使います。 ５． (x+3) を共通因数としてくくり出しましょう。 【解答と解説】 １． 4x²−16x ← 共通因数 4x でくくり出します =4x(x−4) ２． a²+8a+15 ← たして 8 、かけて 15 になる組 (3,5) を見つけます =(a+3)(a+5) ３． 25x²−16y² ←(2乗)ー(2乗) の形にします =(5x)²ー(4y)² ← 公式④を使います =(5x+4y)(5x-4y) ４． 3x²−30x+75 ←共通因数 3 をくくり出します =3(x²−10x + 25) ← かっこの中で、公式③を使って因数分解します =3(x−5)² ５． (x+3)²−5(x+3) ←共通因数 (x+3) をくくり出します =(x+3){(x+3) - 5} ← かっこの中を整理します =(x+3)(x - 2) まとめと商品紹介 いかがでしたか。因数分解の基本を理解したら、あとは定着させるために練習あるのみです。 因数分解の知識を確かな力に変えるために、あなたのレベルに合った文理の教材で次のステップに進みましょう！ おすすめの商品 因数分解の基本と応用を理解したら、あとは練習あるのみです。 文理では、お客様ひとりひとりのレベルや目的に合わせた教材をご用意しています。 ここでは、あなたの学習を次のステップに進めるための、おすすめの商品を3シリーズご紹介します。 わからないをわかるにかえる ▶シリーズページはこちら ▶ご購入はこちら 因数分解を基礎からじっくり学びたい、これまでどこから手をつけていいかわからなかったという人に最適なシリーズです。 この教材は、「わからない」を「わかる」にかえることを徹底的に追求しています。 定義や公式といった基礎的な内容を、簡単な例題で丁寧に解説しているため、因数分解が苦手な人でも、着実に基礎から練習を積み重ねることができます。 簡単なステップで自信をつけながら学習を進めたい方に、特におすすめします。 完全攻略 ▶シリーズページはこちら ▶ご購入はこちら 因数分解の知識を深め、確かな実力をつけたいなら「完全攻略」シリーズが役立ちます。 このシリーズは豊富な演習量が特徴で、基礎の反復から応用までしっかりと問題演習をこなすことで、因数分解を完全に理解し、定着させることができます。 また、定期テスト対策ページや、過去の入試問題を扱った実戦問題ページも収録されているため、日々の学習から受験対策まで幅広い学習に対応可能です。 学校の授業の進度に合わせて使いたい方にも最適です。 ハイクラス徹底問題集 ▶シリーズページはこちら ▶ご購入はこちら 難易度の高い問題に挑戦し、数学の応用力を圧倒的につけたい人向けの最高峰の問題演習集です。 この問題集では、因数分解の複雑な応用問題や、複数の知識を組み合わせる思考力を要する問題を豊富に扱っています。 難関高校の入試問題も収録されているため、ハイレベルな演習を通じて、ライバルに差をつけたいと考えている学習者を徹底的にサポートします。 現在の学習レベルに関わらず、数学を極めたいという意欲のある方は、ぜひ手に取ってみてください。
