2025/10/03
【中学生向け】因数分解のやり方と公式一覧 テストで使えるコツも解説
はじめに
今回のテーマは中学3年生の数学で出てくる「因数分解」です。
「因数分解」という言葉を聞いて、
「難しそう…」
「公式がたくさんあって覚えられない！」
と感じている人もいるかもしれません。
しかし、心配はいりません！
因数分解は、中学数学の大きな柱ですが、正しい手順といくつかのコツさえつかめば、必ず理解できるようになります！
この記事では、因数分解が「なぜ大切なのか」という基礎から、テストで使える4つの公式、さらには応用問題の解き方まで、ステップごとにわかりやすく解説します。
この記事を最後まで読んで、因数分解への理解を深め、定期テストや高校入試で自信を持って問題が解けるようになりましょう！
因数分解とは？
因数分解とは、簡単に言うと「多項式をかけ算の形（因数の積の形）になおす操作」のことです。
まずは因数について確認しましょう。
例えば、6という数は、次のようにかけ算の形になおすことができますね。
6=2×3
このとき、2や3を6の因数と呼びます。
因数分解とは、多項式をいくつかの因数の積の形に分解することです。
【例】 2a2+6ab=2a(a+3b)
左側の式 2a2+6ab はたし算（単項式の和）の形ですが、
右側の式 2a(a+3b) は、2 と a と (a + 3b) という因数のかけ算の形になっています。
展開と因数分解の関係
因数分解を理解する上で、展開（てんかい）との関係を知っておくことが大切です。
因数分解は、展開の逆の操作だと考えると、イメージがしやすいでしょう。
展開：かけ算を計算して、たし算・ひき算の形になおすこと
(x+2)(x+3) ― 展開 → x2+5x+6
因数分解：たし算・ひき算の形を、かけ算の形になおすこと
x2+5x+6 ― 因数分解 → (x+2)(x+3)
このように、展開と因数分解は、「たし算・ひき算の形」と「かけ算の形」を行き来する、裏表の関係になっています。
このイメージを持っておくと、公式を理解する際にも役立ちます。
なぜ因数分解を学ぶのか
「わざわざ式をかけ算の形になおすのはなぜ？」
と思うかもしれません。
ここでは、因数分解を学ぶ理由を3つ紹介します。
• 2次方程式を解くため
x2+5x+6=0
のような2次方程式の解を求めるときは、左辺を因数分解をして、
(x+2)(x+3)=0
の形になおすことで、
x=−2 または x=−3
という解を求めることができます。
• 計算を簡単にするため
複雑な多項式を因数分解してシンプルな形にすることで、計算ミスを防ぐことにつながります。
特に、「式の値」を求めるときに役立ちます。
【例】 x=98のとき、x2+4x+4 の値を求めましょう。
直接代入して求めることもできますが、
982+4×98+4
を計算するのはたいへんです。
そこで、先に因数分解をして (x+2)2 にしてから代入します。
(98+2)2 = 1002 = 10000
と、計算が簡単になります！
• 高校数学の基礎となるため
高校で学ぶより高度な数学（数Ⅱ、数Bなど）でも、因数分解は当たり前の基礎技術として使われます。
今のうちにしっかり身につけておくことが、将来の数学の土台となります。
因数分解は、定期テストでも高校入試でも必ず頻出する重要な分野です。
しっかり理解を深め、数学の基礎力を身につけましょう！
因数分解の解き方：共通因数でくくる
ここからは、因数分解の解き方についてです。
因数分解をするとき、まず最初に考えるべきなのが、「共通因数でくくる」という方法です。
共通因数でくくるとは？
共通因数とは、多項式のすべての項に共通してかけられている数や文字のことです。
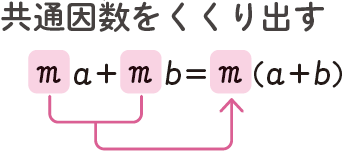
多項式を、共通因数と残りの部分の積の形になおす操作を、「共通因数でくくる」「共通因数でくくり出す」と言います。
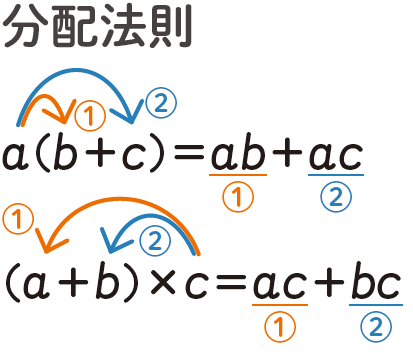
これは、展開のときの分配法則の逆の操作です。
【例】 2x+6 を因数分解しましょう。
１．共通因数を見つける
それぞれの項 ( 2x と 6 ) の中に共通して含まれている因数を探します。
2x=2×x
6=2×3
両方の項に共通しているのは、2 です。
つまり、共通因数は 2 です。
２．共通因数でくくる
共通因数 2 を式の前に出し、かっこでくくります。
2x+6=2(x+3)
符号と文字の扱いに注意する
多項式の最初の項がマイナスのときは、マイナスも共通因数の一部としてくくり出すことが多いです。
特に、共通因数に文字も含まれる場合は注意が必要です。
【例】 −3ab+12bを因数分解しましょう。
この式は、共通因数として数(係数)と文字の両方に着目します。
１．共通因数を見つける
数(係数)の部分 ： −3 と +12 の共通因数は −3
文字の部分 ： ab と b の共通因数は b です。
したがって、共通因数は −3b です。
２．共通因数でくくる
−3ab+12b=−3b(a−4)
【注意】
マイナスでくくると、かっこの中の項の符号がすべて逆になることに注意しましょう。
○ −3ab+12b=−3b(a−4)
× −3ab+12b=−3b(a＋4)
因数分解の解き方：４つの公式
共通因数でくくれない場合、次に因数分解の4つの公式を使います。
これらは、展開の公式を逆にしたものです。
展開の公式をしっかり覚えていると、スムーズに理解できます。
公式① x²+(a+b)x+ab=(x+a)(x+b)
これは「たして (a+b)、かけて ab」になる a と b の組み合わせを見つける公式です。
【式の形】
x の項の係数が a+b(和）、定数項が ab(積）になっているのが特徴です。
【解き方のコツ】
１．まず、定数項 ab に注目し、積になる a と b のペアを考えます。
２．そのペアの中で、和が x の項の係数 (a+b) になるものを見つけます。
３．見つけた a と b を (x+a)(x+b) の形に当てはめます。
【例】 x2+7x+12 を因数分解しましょう。
１．積が 12 になるペアを探します。 (1, 12)、(2, 6)、(3, 4) …
２．その中で、和が 7 になるペアはを見つけます。 (3, 4)
３．x2+7x+12=(x+3)(x+4)
公式② x²+2ax+a²=(x+a)² 公式③ x²－2ax+a²=(x－a)²
これらは、「和の平方」「差の平方」と呼ばれる公式です。
公式①で、 a=b の特殊なパターンと考えると理解しやすいでしょう。
【式の形】
xの項の係数が 2a ( a の2倍)、定数項が a2 ( a の2乗) になっているのが特徴です。
（※公式③は符号がマイナスです。）
【解き方のコツ】
１．定数項が、ある数 a の2乗になっていることを確認します。
２． x の項の係数が、1で確認したaの2倍になっているかを確認します。
３．符号に注意して (x±a)2 の形になおします。
【例】 x2−10x+25 を因数分解しましょう。
１．定数項 25 は 52 、または (−5)2 です。
２．xの項の係数 −10 は、−5 の 2 倍なので、公式③で a=5 のときだとわかります。
３．x2−10x+25=(x−5)2
公式④ x²−a²=(x+a)(x－a)
(2乗)ー(2乗) の形をした因数分解の公式です。
公式①で、 b=ーa の特殊なパターンと考えると理解しやすいでしょう。
【式の形】
x の項の係数が 0 になっていて、項が2つしかないのが大きな特徴です。
【解き方のコツ】
１．式が (2乗)ー(2乗) の形になっているかを確認します。
２．(x+a)(x−a) の形に当てはめます。
【例】 x2−49 を因数分解しましょう。
１． 49 は 72 なので、x2− 72 の形です。
２．x2−49=(x+7)(x-7)
展開公式との関係
公式①から④は、すべて展開公式を逆にしたものです。
因数分解ができたら、展開し直して元の式に戻るか確認する習慣をつけましょう。
これにより、ミスが減り、公式の理解もさらに深まります。
x2+7x+12 ― 因数分解 → (x+3)(x+4)
(x+3)(x+4) ― 展開 → x2+7x+12
因数分解の解き方ステップ
これまでに学んだ「共通因数でくくる」方法と「4つの公式」を使えば、多項式の因数分解ができるようになります。
しかし、問題を見たときにどの方法を使えばいいか迷ってしまうことがありますよね。
ここでは、因数分解のときに迷わず正解にたどり着くためのステップを解説します。
１．共通因数を探す
因数分解を始めるとき、公式が使えるかどうかを確認する前に、必ず共通因数があるかを確認しましょう。
共通因数を見つけてくくり出すことで、その後に使う公式を見つけやすくなります。
【チェックポイント】
すべての項に共通する因数（数や文字）はないか？
【注意点】
共通因数をくくり出すのを忘れると、完全に因数分解された形にたどり着けなくなります。
２．使える公式があるか判断する
共通因数をくくりだしたあと、残った多項式を見て、どの公式が使えるかを判断します。
次のように順序だてて考えましょう。
【項が２つ】
→ 公式④ x²−a²=(x+a)(x－a)
が使えるか確認する
【項が３つ】
→ 【定数項が a² の形になっている】
→ 公式② x²+2ax+a²=(x+a)²
公式③ x²－2ax+a²=(x－a)²
が使えるか確認する
→ 【定数項が a² の形になっていない】
→ 公式① x²+(a+b)x+ab=(x+a)(x+b)
が使えるか確認する
工夫して分解する応用パターン
共通因数やくくり出し、公式を組み合わせることで解ける応用問題のパターンをいくつかご紹介します。
「これ以上分解できない」状態まで分解しきるのが因数分解のゴールです。
１．複雑な式は展開してから分解する
元の式が複雑なかっこのかけ算の形になっている場合、まずは展開して同類項をまとめることで、公式が使える形になることがあります。
【例】 (x+3)(x−1)−12 ← 展開の公式を使って展開します
=x²+2x−3−12 ← 同類項をまとめます
=x²+2x−15 ← たして +2、かけて -15 になる数（5，－3）を探して、公式①を使います
=(x+5)(x−3)
２．多項式を共通因数としてくくり出す
共通因数が数や文字ではなく、多項式になる場合もあります。
多項式全体を１つのかたまりと考えて、共通因数をくくり出します。
一見共通因数がないように見えても、一部を因数分解すると共通因数が見つかることがあります。
【例】 5(a−2)+a²−2a ← 5(a−2) と a²−2a に分けて考え、後ろの式で a をくくり出します
=5(a−2)+a(a−2) ← 多項式 (a−2) が共通因数になっているので、くくり出します
=(a−2)(5+a)
３．共通因数をくくり出してから公式を使う
共通因数でくくり出したあと、さらに因数分解できる場合があります。
因数分解できるかどうか、必ず最後までチェックしましょう。
【例】 3x³y−12xy³ ← 共通因数 3xy でくくり出します
=3xy(x²−4y²) ← x²−4y² で、公式④を使って因数分解します
=3xy(x+2y)(x－2y)
４．x² の項の係数が1でない式
x² の項の係数が常に1とは限りません。
そんな式でも、公式②または③が使える場合があります。
何かの2乗になっているか考えるのがポイントです。
【例】 9x²−6xy+y² ← 公式が使える形に変形します
=(3x)²−2×3x×y+y² ← 公式③を使います
=(3x−y)²
練習問題で確認しよう
これまでの知識が定着しているか、以下の問題で確認してみましょう。
因数分解は、「共通因数」→「公式」の順番で考えることが大切です！
【問題】 次の式を因数分解しましょう。
１．4x²−16x
２．a²+8a+15
３．25x²−16y²
４．3x²−30x+75
５．(x+3)²−5(x+3)
【ヒント】
解き方に迷ったら、以下のヒントを参考にしてください。
１．まずは、数と文字の共通因数を見つけて、くくり出しましょう。
２．公式①のパターンです。たして +8、かけて +15 になる2つの数を探しましょう。
３．(2乗)ー(2乗) の形です。公式④を使いましょう。
４．最初に共通因数の3をくくり出し、かっこの中の式で公式③を使います。
５． (x+3) を共通因数としてくくり出しましょう。
【解答と解説】
１． 4x²−16x ← 共通因数 4x でくくり出します
=4x(x−4)
２． a²+8a+15 ← たして 8 、かけて 15 になる組 (3,5) を見つけます
=(a+3)(a+5)
３． 25x²−16y² ←(2乗)ー(2乗) の形にします
=(5x)²ー(4y)² ← 公式④を使います
=(5x+4y)(5x-4y)
４． 3x²−30x+75 ←共通因数 3 をくくり出します
=3(x²−10x + 25) ← かっこの中で、公式③を使って因数分解します
=3(x−5)²
５． (x+3)²−5(x+3) ←共通因数 (x+3) をくくり出します
=(x+3){(x+3) - 5} ← かっこの中を整理します
=(x+3)(x - 2)
まとめと商品紹介
いかがでしたか。因数分解の基本を理解したら、あとは定着させるために練習あるのみです。
因数分解の知識を確かな力に変えるために、あなたのレベルに合った文理の教材で次のステップに進みましょう！
おすすめの商品
因数分解の基本と応用を理解したら、あとは練習あるのみです。
文理では、お客様ひとりひとりのレベルや目的に合わせた教材をご用意しています。
ここでは、あなたの学習を次のステップに進めるための、おすすめの商品を3シリーズご紹介します。
わからないをわかるにかえる
因数分解を基礎からじっくり学びたい、これまでどこから手をつけていいかわからなかったという人に最適なシリーズです。
この教材は、「わからない」を「わかる」にかえることを徹底的に追求しています。
定義や公式といった基礎的な内容を、簡単な例題で丁寧に解説しているため、因数分解が苦手な人でも、着実に基礎から練習を積み重ねることができます。
簡単なステップで自信をつけながら学習を進めたい方に、特におすすめします。
完全攻略
因数分解の知識を深め、確かな実力をつけたいなら「完全攻略」シリーズが役立ちます。
このシリーズは豊富な演習量が特徴で、基礎の反復から応用までしっかりと問題演習をこなすことで、因数分解を完全に理解し、定着させることができます。
また、定期テスト対策ページや、過去の入試問題を扱った実戦問題ページも収録されているため、日々の学習から受験対策まで幅広い学習に対応可能です。
学校の授業の進度に合わせて使いたい方にも最適です。
ハイクラス徹底問題集
難易度の高い問題に挑戦し、数学の応用力を圧倒的につけたい人向けの最高峰の問題演習集です。
この問題集では、因数分解の複雑な応用問題や、複数の知識を組み合わせる思考力を要する問題を豊富に扱っています。
難関高校の入試問題も収録されているため、ハイレベルな演習を通じて、ライバルに差をつけたいと考えている学習者を徹底的にサポートします。
現在の学習レベルに関わらず、数学を極めたいという意欲のある方は、ぜひ手に取ってみてください。
関連記事
素数とは？中学数学で押さえておきたいポイント
もくじ 素数って何？基本を知ろう 素数は中学数学でどのように使うの？ 素数を見分ける方法 素数に関するよくある質問 素数の面白い応用例 「わからないをわかるにかえる数学」 「大人の教科書ワーク 数学」 まとめ 素数って何？基本を知ろう 素数の定義をわかりやすく 素数とは、「１とその数自身の積でしか表せない自然数のこと」です。 言い換えると、「１とその数以外に約数ををもたない（約数が２つの）自然数」が素数となります。 ２、３、５、７、・・・ などが素数ですが、例えば７は、１と７でしか割り切れませんから、素数です。 ４や６は、１とその数自身でも割り切れますし、それぞれ２と３でも割り切れますので、素数ではありません。 素数を中学数学で学ぶ理由 素数は、数学の基礎となり、中学数学・高校数学を学ぶうえで必要不可欠な知識となります。 中学では、素数は「素因数分解」や「平方根」で使います。 自然数を素数の積だけで表す素因数分解では、言うまでもなく素数が重要な役割をもっています。 また、小学校５年生で習う「最大公約数・最小公倍数」でも、実は素数が鍵となっています。 数学の基礎となる素数はしっかりと理解を深めておく必要があります。 素数は中学数学でどのように使うの？ 素因数分解で使う例 自然数を素数の積だけで表すことを素因数分解といいます。 素因数分解の基本手順はしたのようになります。 したがって、８４を素因数分解すると、２×２×３×７となります。（実際の問題に答える際には、２²×３×７としましょう。） 最大公約数・最小公倍数の計算での役割 先ほど、最大公約数・最小公倍数で素因数分解が使えると書きましたが、どのように使うのでしょうか。 たとえば、９０と１６２の最大公約数と最小公倍数を考えます。 ９０と１６２をそれぞれ素因数分解すると、こうなります。 これを、下のように縦にそろえて書きます。 ９０と１６２の最大公約数は、したのように考えて、１８だということがわかります。 ９０と１６２の最小公倍数は、したのように考えて、８１０だということがわかります。 このように、最大公約数や最小公倍数を求める際には、素因数分解が役立ちます。 素数を見分ける方法 小さな数で割り算してみる 素数かどうかを見分けるために、小さな数で割り算をしてみるという方法があります。 【手順】 １. まず２で割ってみる 偶数はすべて２で割り切れるので、２以外の偶数は素数ではありません。 例：４、６、８…は２で割り切れるので素数ではない。 ２. 次に３で割る ３で割り切れる場合、その数も素数ではありません。 例：９、１２、１５…は３で割り切れるので素数ではない。 ３. ５で割る 最後の数字が０か５で終わる数は、５で割り切れるため、素数ではありません。 例：１０、１５、２０…は５で割り切れるので素数ではない。 ４. ７、１１、１３、１９…と暗記している素数で割る エラトステネスの篩（ふるい）を使う方法 こちらの方法は、中学数学では習わないのですが、 「エラトステネスのふるい」という名の通り、ふるいにかけるように、多くの数のなかから素数を見つけのに便利です。 この方法を使って、1～40までの範囲の素数を見つけてみましょう。 【手順】 １. １を消す ２. 最も小さい素数を残したまま、その素数の倍数をすべて消す。 この場合は、２を残して、２以外の２の倍数をすべてふるい落とします。 ３. 残っている中で最も小さい素数を残したまま、その素数の倍数をすべて消す この場合は、３を残して、３以外の３の倍数をすべてふるい落とします。 ４. 手順３を最後まで繰り返す。 ４はすべてふるい落とされているので、５を残して、５以外の５の倍数をすべてふるい落とします。 最後まで繰り返すと、下図のようになります。 中学のテストでよく出る素数判定問題 中学のテストでは、ある数が素数かどうかを見分ける問いがよく出題されます。 例えば、 問題：101は素数か答えなさい 解答：101の約数は「１」と「１０１」の２つなので、１０１は素数である。 などです。 上記で紹介した方法などを用いて、素数かどうかを見分けます。 中学では覚えておくべき素数 中学の問題では、少なくとも【２,３,５,７,１１,１３,１７,１９】あたりまでの素数を暗記しておくとよいでしょう。 暗記をしておくことで、素数を見分ける問題が楽に解けるようになります。 もちろん、素数はずっと続いていきますので、興味があれば暗記してみても面白いかもしれないですね。 素数に関するよくある質問 ・１は素数じゃないの？ 素数の定義をみてみると、「１とその数以外に約数ををもたない（約数が２つの）自然数」となっています。 たとえば、２の約数は１と２の２つ、７の約数は１と７の２つ。 １は、約数が１自身の１つだけしかないので、素数ではないということになります。 ・なぜ2は素数なのか？ なんとなく、２は偶数だから素数ではない気がしてしまいますが、２は素数です。 ２は、「１」と「２」自身の２つの約数をもつ自然数なので、２は素数となります。 うっかりミスで、２が素数ではないと勘違いしないようにしましょう。 ・素数は無限にあるの？ 素数は無限に存在します。 素数が無数に存在することの証明は、色々な方法でされています。 有名なのは、背理法によるユークリッドの証明です。こちらは紀元前に発見されたものです。 そのほかにも、フェルマー数を用いたゴールドバッハの証明や、2006年に発表されたサイダックの証明などがあります。 ・素数は何年生で学ぶ？ 素数は、中学１年生で学びます。 現行の学習指導要領では、素数を１年において扱うことにより、 素因数分解を自然数、素数、倍数、約数、公倍数、公約数などと関連づけ、 整数の性質を探るひとつの道具として利用することができるとしています。 参考：文部科学省「中学校学習指導要領(平成29年告示)解説」2017年 ▼文部科学省ホームページ 中学校学習指導要領解説：文部科学省 ・100までの素数リストは？ １～１００までに、素数は 「 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97」があり、全部で25個あります。 下図の白い背景のマスが、素数です。 素数の面白い応用例 素数は、とても不思議な数字です。 身近でも、素数の面白い応用例や、素数に絡んだ不思議なことがたくさんあります。 インターネットの暗号に使われる素数 インターネット上の情報を守るのに「暗号化」という技術が使われていますが、この暗号化において素数が重要な役割を担っています。 とある文書があったとき、素数×素数のかけ算で文書に暗号をかけます。 第三者には、かけ算の結果が公開されています。 暗号を元の文書に戻すためには別の鍵が必要です。 この鍵を得るためには、自然数＝素数×素数と、逆の計算をしなければいけません。 地道に計算するので、素数の桁が大きいほど大変です。 簡単な例で考えると、１９×２３のかけ算はひっ算を使えばすぐできるけど、437＝19×23を逆の計算をするのは大変ですよね。 この作業は、コンピューターでも膨大な時間がかかるため、インターネットのセキュリティでは素数が重要な役割を担っているということです。 自然界の不思議：セミと素数の関係 素数ゼミとよばれるセミを聞いたことがあるでしょうか。 素数ゼミとは、生き残り戦略のために、１３年、もしくは１７年の間、地中にいるセミのことです。 それでは、なぜ素数である１３年、もしくは１７年の間、地中にいることが生き残り戦略となるのでしょうか。 その秘密は、最小公倍数にあります。 例えば、１３年ゼミ周期で土の中から出てくる素数ゼミに、３年周期で発生する天敵がいたとします。 天敵が３年周期で発生していても、同じ年に１３年周期ゼミが地上に出るのは、上の表のように３９年経ったときのみです。 ３９は、１３と３の最小公倍数です。１３が素数であるため、３を約数に持たないことから、この最小公倍数が大きくなっています。 仮にセミの地上にいる期間が１年短い１２年だとすると、地上に出れば毎回３年周期で発生している天敵がいるということになってしまいます。 セミの発生周期が素数であることは、その数自身しか約数がない自然数である素数を地上にでる周期にすることで、 天敵とできるだけ出会わないようにする、セミの生き残り戦略と考えることができます。 「わからないをわかるにかえる数学」 ここでPR！ 今回解説した「素数」は中学１年生で学びます。 そんな中学生向けの中学生向けの超基礎シリーズが、こちらの『わからないをわかるにかえる』。 平易な言葉でイラスト豊富に解説し、問題量も多すぎないので学び直しにも活用できます。 ▶シリーズページはこちら ▶ご購入はこちら 「わからないをわかるにかえる高校入試数学」 人気の超基礎シリーズ「わからないをわかるにかえる」の高校入試対策版です。 中学3年間の内容を基礎からおさらいできます。 やさしい言葉遣いやイラストで、とっつきやすいのが特徴で、苦手な分野が多く、易しめから入りたい人はチェックしてみてください。 ▶シリーズページはこちら ▶ご購入はこちら 「大人の教科書ワーク 数学」 日常の悩みや疑問を、小中学校の教科書で解決！ それがこちらの『大人の教科書ワーク』です。 実は、今回の記事のなかで紹介した「インターネットの暗号に使われる素数」や「セミと素数の関係」について、 この『大人の教科書ワーク数学』ではさらに詳しく書かれています！ この本では、このような数学にまつわる面白いトピックをたくさんとりあげています。 「大人の学び直し」がテーマの本ですが、小中学校の教科書で習う算数・数学の内容を用いながら、 日常のあらゆる疑問に答える形式になっているので、いままさに数学を学んでいる中学生が数学を学ぶ楽しさを知るのにもぴったりです！ ▶シリーズページはこちら ▶ご購入はこちら まとめ いかかでしたか。 今回の記事では、素数の定義から中学数学で押さえておきたいポイント、素数を応用した例までご紹介しました。 素数は数学の基礎であると同時に、どこか不思議な数字ですよね。 素数を通じて数学の魅力に触れ、ぜひ今の学びを深めてみてください！
中学生応援コラム 第1回「高校入試のとらえ方(1) 種別と学科」
皆さん、こんにちは！ 金澤 浩です。 このコラムでは、中学生が学校の勉強をスムーズに進め、良い高校入試を迎えるサポートができればと思い、学校の勉強や入試に向けて取り組むべきポイントを全10回でお伝えしていきたいと思います！ 今までの更新コラム 第1回「高校入試のとらえ方(1) 種別と学科」第2回「高校入試の捉え方(2) 受験形態」第3回「内申ってなんだろう 高い内申をとるために必要なこと」第4回「内申点と将来の選択肢への影響」 第5回「定期テストってなんだろう 高得点を取るために必要なこと」 第6回「定期テスト成功の秘訣！普段から意識したいこと」 第7回「模擬試験はできるだけ早くから受けよう！」 第8回「勉強と部活の両立をどう捉えるか」 第9回「高校の選び方とその先」 第10回「自主性と主体性」 1回目はこれから高校入試を迎えるにあたって、今から考えておいてほしいポイントをお伝えします。 最初に考えることは 高校入試にあたって最初に考えるべきは「高校の種別」をどうするか、というテーマです。 大きな方向性として考えるべきことは二つで、一つは公立か私立か、もう一つは学科をどうするか（普通科かそれ以外か）、ということです。 公立と私立の違い 公立と私立の違いについて、皆さんはいくつ挙げられるでしょうか。 学費に大きな違いがあるのはご存知の方も多いかもしれません。 私立は高いというイメージがおありでしょうが、今では国から「就学支援金」という学費支援があり（所得条件等あり）、私立もかなり通いやすくなっています。 他の違いで重要な点としては「教育内容」「教員」「施設・設備」などがあります。 公立と比べて私立は各学校の理念やスタンスに特色があるため、教育内容や取り組みも特徴的になりやすく、校風や生徒対応も学校によってかなり違います。 教員も公立の場合は数年で異動がありますが、ほとんどの私立では異動がないため教育の特徴を継続的にしやすい点も大きな違いです。 施設・設備も学校の理念や特色に合わせて違いがあり、グラウンドが広いとか、変わった特別教室があるとか、いろんな特色が際立っているのが私立の特徴です。 学科の選択 学科の選択も非常に重要なポイントです。 普通科は大学進学をベースに幅広く様々な学習を行い、進路選択の柔軟性を広く保つのが特徴です。 それ以外の学科の選択肢は多種多様で、よくある例だと商業・工業・理数・国際など、変わったところだとビジネスや舞台芸術などかなり専門分野に特化した学科もあります。 また、幅広く学んだり専門分野を深めたりという柔軟性の高いのが総合学科で、近年高校数が増えてきています。 興味のある分野があったり、専門的に強い分野を作りたかったり、という場合は普通科ではない方向性が向いているでしょう（理数系に特化するなら「高等専門学校」という選択肢もあります）。 大切なのは・・・？ 一番伝えたいことは、「高校は義務教育ではない」ということ。 そもそも行くかどうかも決めていいですし、どんな選択肢を選んでもいいのです。 こうあるべき・こうした方がいいという大人の考え方も大切ですし、同時に本人がどういうことを学びたいか・どんな方向に進んでいきたいかを考えることも非常に大切なのです。 ぜひ高校入試を機会として、子どもの将来を真剣に話し合ったり、実際に学校に足を運んだりしてほしいと思います！ 次回ももう少し高校入試のことについてご説明しようと思います。 入試制度や受験制度について、中学で力を入れるべきことについてお伝えします。 筆者：金澤 浩（かなざわ ひろし） 大手学習塾で20年以上指導し、様々な生徒を合格に導く。現在は共育コンサルタントとして講演会や個別での進路選択や学習の支援に取り組む
小学生でもわかる！パーセント計算のやり方とコツ
もくじ はじめに パーセントとは？ パーセント計算の基本ルール 割引や増加・減少とパーセント計算 パーセントの計算をもっと楽しくするコツ 計算が得意になる！ おすすめ問題集 まとめ はじめに 「この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は…」 「水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何％かな？」 「この服、4500円だけど30%オフになっているよ！いくらになるのかな？」 私たちの生活の中には、パーセント(%)という言葉がたくさん出てきます。 パーセントを理解すると、身の回りのことがよくわかるようになります。 この記事では、小学生のみなさんにもわかりやすいように、パーセントの基本的な考え方、計算方法、ちょっとしたコツなどを紹介します。 パーセントの世界を一緒に探検してみましょう！ パーセントの計算ができる文理のドリルシリーズはこちら！ できる!!がふえる↑ドリル ハイレベル算数ドリル 小学教科書ドリル パーセントとは？ ◆パーセントの意味 普段の生活の中でパーセント(%)という記号をよく見かけますよね。 これは、 「全体を100としたときにどのくらいあるか」 を表す記号です。 「％」を使って表す割合を、百分率といいます。 全体を100(百)としているので百分率です。 たとえば、全体で100人いる中で、20人がめがねをかけているとき、めがねをかけている人は「20%」になります。 全体を100として考えることで、全体の数が半端な数であっても、どのくらいあるかわかりやすくなります。 ◆割合、歩合、百分率の関係 百分率と合わせて、割合や歩合という言葉も使われます。 これは、全体を何にするかで使い分けます。 ・割合 → 全体を1としたときにどのくらいあるか。 単位はつけません。 ・歩合 → 全体を10としたときにどのくらいあるか。 単位は割(わり)、分(ぶ)、厘(りん)などを使います。 ・百分率 → 全体を100としたときにどのくらいあるか。 単位は％です。 割合を10倍すると歩合、割合を100倍すると百分率になります。 具体例で確認してみましょう。 全体で100人いる中で、20人がめがねをかけているとき、 ・割合 → 0.2 (20÷100=0.2) ・歩合 → 2割 (20÷100×10=2) ・百分率 → 20% (20÷100×100=20) となります。 ３つの関係を表にまとめると、関係がわかりやすくなります。 歩合が使われることは減っていますが、野球の打率を表すときに使われます。 例：文理野球部４番バッターの今年の打率は、3割ちょうどでした。 この場合、このバッターは、10打席中３打席ヒットやホームランを打つと考えられます。 パーセント計算の基本ルール ◆「○○の□□％」を計算する方法 ここからは、テストでもよく出る問題の解き方を、パターン別に解説します。 解き方を確認したら、練習問題にもチャレンジしてみましょう！ 例題 400円の20％は？ 解き方・答え 計算するときは、百分率を割合に直します。 20% → 0.2 (20÷100=0.2) 400×0.2＝80(円) 20のまま計算しないよう注意しましょう。 では、練習問題です！ 練習問題 ★次の計算をしましょう。 １．800gの20％は？ ２．600Lの30％は？ ３．700人の15％は？ ４．この500mLの飲み物に果汁10%って書いてあるよ。ということは果汁の量は… ↑４は、はじめにで紹介した問題です！ 解き方・答え １．20% → 0.2 800×0.2=160(g) ２．30% → 0.3 600×0.3=180(L) ３．15% → 0.15 700×0.15=105(人) ４．10% → 0.1 500×0.1=50(ｍL) パーセントを使って計算するときは、百分率を割合に直すことを忘れないようにしましょう。 ◆「□□は○○の何％？」を計算する方法 次は、割合を計算してからパーセントを求める問題です。 例題 80円は400円の何％？ 解き方・答え まず、割合を求めます。 80÷400=0.2 何％か求めるので、100をかけて百分率に直しましょう。 0.2×100=20(%) では、練習してみましょう！ 練習問題 ★次の計算をしましょう。 １．50gは200gの何％？ ２．48Lは80Lの何％？ ３．150人は1250人の何％？ ４．水に食塩6gを混ぜたら300gの食塩水ができたよ。食塩水の濃度は何％かな？ 解き方・答え １．50÷200=0.25 0.25×100=25(%) ２．48÷80=0.6 0.6×100=60(%) ３．150÷1250=0.12 0.12×100=12(%) ４．6÷300=0.02 0.02×100=2(%) 百分率(パーセント)で答えるので、100をかけて百分率に直すことに注意しましょう。 割引や増加・減少とパーセント計算 ◆割引とパーセント お店で買い物をするときに、「30%オフ！」というPOPを見かけることはありませんか？ これは、元の値段から30%安くなることを表しています。 割引されるときのパーセントの計算を確認しましょう！ 例題 5000円の服が40%オフで売られています。支払う金額はいくらですか？ 解き方・答え 40%が0.4であることに注意して、まずは安くなる金額を求めます。 5000×0.4=2000(円) 次に、支払う金額を求めます。 5000-2000=3000(円) では、練習してみましょう。 練習問題 ★次の問題に答えましょう。 １．800円のお菓子が15%オフで売られています。支払う金額はいくらですか？ ２．2500円の商品が20%オフになっています。支払う金額はいくらですか？ ３．定価12000円の自転車が35%オフで売られています。支払う金額はいくらですか？ ４．この服、4500円だけど30%オフになっているよ！いくらになるのかな？ 解き方・答え １．800×0.15=120(円) 800-120=680(円) ２．2500×0.2=500(円) 2500-500=2000(円) ３．12000×0.35=4200(円) 12000-4200=7800(円) ４．4500×0.3=1350(円) 4500-1350=3150(円) ◆増える・減るときのパーセント 増えたり減ったりするときにもパーセントは使われます。 例題 タケルさんの今回のテストの点数は、前のテストの点の80点より15%増えました。 今回のテストは何点でしたか？ 解き方・答え まず、増えた点数を求めます。 80×0.15=12(点) 次に、今回の点数を求めます。 80+12=92(点) では、練習問題です！ 練習問題 ★次の問題に答えましょう。 １．ユイさんの身長は、１年前に150cmでしたが、この1年で5%伸びました。今の身長は何cmですか？ ２．A地域の人口は、昨年10000人でしたが、今年は2%減りました。A地域の今年の人口は何人ですか？ ３．お父さんの体重は60kgでしたが、ダイエットをして10%減らしました。ダイエット後の体重は何kgですか？ 解き方・答え １．150×0.05=7.5(cm) 150+7.5=157.5(cm) ２．10000×0.02=200(人) 10000-200=9800(人) ３．60×0.1=6(kg) 60-6=54(kg) より多くの問題を解きたい方はこちら！ できるが!!ふえる↑ドリル ハイレベル算数ドリル 小学教科書ドリル パーセントの計算をもっと楽しくするコツ ◆暗算のちょっとしたテクニック ここからは、知っていると便利なテクニックを紹介します。 よく出るパーセントの計算方法を覚えておくと、暗算で答えが出せるようになることがあります。 ・10% → 元の数を10でわるのと同じ！ 例：290円の10%は？ 290÷10=29(円) ・50% → 元の数を2でわるのと同じ！ (元の数の半分！) 例：800個の50%は？ 800÷2=400(個) ・25% → 元の数を4でわるのと同じ！ (元の数の4分の1！) 例：200ページの25%は？ 200÷4=50(ページ) ・20% → 元の数を5でわるのと同じ！ 例：500mLの20%は？ 500÷5=100(mL) これらのテクニックを覚えておくと、暗算できることがあります。 ◆クイズでパーセントをマスターしよう！ ここまで学習してきたパーセントの計算を使って、クイズに答えてみましょう。 問題 ★次の問題に答えましょう。 １．定価1000円のものが60%オフで売られています。 財布に500円しかないとき、この商品を買える？買えない？ ２．50点満点のテストの結果が40点でした。90%正解したことになる？ ３．果汁20%の飲み物を２本買って混ぜたら、果汁は40%になる？ ４．450円の80％と、700円の50％では、どちらが安い？ 解き方・答え １．1000×0.6=600(円) 1000-600=400(円) 500円あるので買えます。 答え 買える。 ２．40÷50=0.8 0.8 → 80% 答え 90%正解したことにはならない。 ３．果汁20%の飲み物を何本混ぜても、果汁は20%のままです。 答え 果汁40%にはならない。 ４．450×0.8=360(円) 700×0.5=350(円) 答え 700円の50％の方が安い。 計算が得意になる！ おすすめ問題集 文理の書籍には、計算練習ができるものがたくさんありますので紹介します。 今回紹介したパーセントの計算以外の計算問題もたくさんあります。 計算力をつけるには問題をたくさん解くことが一番！ 力をつけたい方はぜひチャレンジしてみてください。 ※パーセントの問題は、小学5年生で詳しく学習します。 パーセントの問題を練習したい方は、小学５年生の書籍をご利用ください。 ◆小学教科書ワーク 「算数」 教科書に完全対応しているから、学校の授業に合わせて使いやすい！ 計算練習ノート、ポスター、動画、CBTなど付属品も充実！ 全教科書に対応した「数と計算」「文章題・図形」シリーズも用意しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆小学教科書ドリル 「算数」 1回10分で終わるドリルだから、習い事など忙しくても続けやすい！ 基本・確認の２ステップで、無理なく力がつきます！ 計算問題に特化した「計算編」文章題や図形問題に特化した「文章題、数・量・図形」シリーズも用意しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆できる!!ふえる↑ドリル １枚ずつはがして使えるから、学習しやすい！ 「計算」「文章題」「数・量・図形」「時こくと時間」など、分野別のシリーズが充実しています。 ▶シリーズページはこちら ▶ご購入はこちら ◆ハイレベル算数ドリル 3段階構成で取り組みやすい！ 詳しい回答解説で、学習をサポート！ ▶シリーズページはこちら ▶ご購入はこちら まとめ 今回の記事では、パーセントの基本的な意味から、計算の仕方、そしてちょっとしたコツまでを解説してきました。 パーセントは、私たちの身の回りの色々なところで使われています。 色々な問題にチャレンジして、パーセントマスターを目指してくださいね！
中学数学の公式をわかりやすくまとめます！高校入試にも役立つ完全ガイド
もくじ はじめに 中学数学で覚えるべき公式とは？ 高校入試で役立つ公式 「なぜそうなるか」から数学公式を理解する 覚え方・使いこなし練習 おすすめの学習教材 まとめ はじめに 「数学の公式って、たくさんあって覚えきれないな…」 「高校入試に向けて、どの公式をしっかり押さえておけばいいんだろう？」 そんな悩みを解消するために、今回は中学数学で学ぶ公式を解説します！ 公式を「知る」から「使える」に変えるための完全ガイド、ぜひ最後まで読んでみてくださいね！ 中学数学で覚えるべき公式とは？ 中学3年間で学習する数学は、主に計算（方程式）、関数、図形の3つの分野に分類できます。 ※データの活用もありますが、今回は公式ということで省略します。 一見するとバラバラに見えるかもしれませんが、実はどれも深いところでつながっています。 学年ごとに確認しましょう。 中1で習う数学公式のポイント 中学1年生になると、算数から数学に教科名が変更され、本格的な数学の学習が始まります。 中学1年生で学習する公式は、この先の数学の土台になりますのでしっかり理解しましょう。 ◆ 正の数・負の数【計算】 四則演算（たし算、ひき算、かけ算、わり算）は、符号ミスに注意することが大切です。 符号の関係を公式としてまとめておくと便利です。 ◆ 文字式【計算】 分配法則は、今後の計算の基本になりますのでここで理解しておきましょう。 割合や速さの関係も、文章題を解く上で大切です。こちらは小学校での学習内容になりますが押さえておきましょう。 ◆ １次方程式【計算】 等式の性質が方程式を解くときの基本になります。移項するときは符号に注意しましょう。 ◆ 比例・反比例【関数】 関係式を公式として整理しましょう。座標の読み取り方も重要です。 ◆ 平面図形・空間図形【図形】 おうぎ形の面積、立体の体積を公式として覚えておきましょう。 おうぎ形は円の一部分だとイメージすると、計算するときに式を思い出しやすくなります。 中2で習う数学公式のポイント 中学2年生では、さらに一歩進んだ内容を学習します。 図形の単元で証明を学習し、ものごとを順序だてて説明する力を養います。 図形に関する公式（定義や定理）が増えますので、正確に理解する力が求められます。 ◆ １次関数【関数】 y=ax+b の形と式の意味、変化の割合などを覚えましょう。高校入試や定期テストでは、図形問題に応用されることも多いです。 ◆ 平行と合同【図形】 平行線と角の関係や、多角形の内角の和・外角の和は、入試の図形問題を解く際にも重要な内容です。 三角形の合同条件は、証明問題を解く際、数多く出てきます。 ◆ 特別な四角形【図形】 平行四辺形、長方形、ひし形、正方形の定義や性質は、小学校で学習した内容でもあります。 中学２年生では、定義、定理として再確認します。 中3で習う数学公式のポイント 中学3年生で学習する公式は、高校入試に直結する重要なものが多くあります。 特に平方根、２次方程式、相似、円、三平方の定理は、入試の頻出単元として強調しておきたいポイントです。 ◆ 多項式【計算】 展開や乗法公式、因数分解の公式が出てきます。因数分解は、２次方程式を解くときにも役立ちます。 ◆ 平方根【計算】 無理数（分数で表すことのできない数）へと数の世界が広がる面白い単元です。 新しい記号であるルートの計算方法を、公式として押さえておきましょう。 ◆ ２次方程式【計算】 主に３つの解き方があります。 因数分解を利用した解き方、解の公式を覚えておくと安心です。 ◆ 相似【図形】 三角形の相似条件は、合同条件との違いを意識して覚えましょう。 線分の比の関係、面積比、体積比は、入試でよく問われます。 ◆ 円【図形】 円や弧を見つけたら、円周角の定理を意識しましょう。 半円の弧に対する円周角が直角(90°)であることも覚えておくと便利です。 ◆ 三平方の定理【図形】 直角三角形の辺の長さの関係を表す定理です。 高校入試頻出で、関数もふくめ、多くの問題で応用されます。 高校入試で役立つ公式 高校入試でよく出る公式を厳選しました。 これらを重点的にマスターし、入試本番で得点アップを目指しましょう。 入試でよく出題される公式には理由があります。 それは、単に知識を問うだけでなく、複雑な問題を解く際に利用したり、他の単元にも応用できるからです。 それでは順番に見ていきましょう。 1. 三平方の定理 図形問題で辺の長さを求めるときに必須です。 平面図形だけでなく、関数や空間図形にも応用されます。 長さを求める問題が出てきたときは、三平方の定理が使えないか意識しましょう。 図形の中にひそむ直角三角形を見つけることがポイントです。 2. ２次方程式の解の公式 因数分解を利用して解けない方程式でも解ける万能な公式です。 因数分解が思いつかなくても焦らなくなります。 3. 関数とグラフの式 直線の式（１次関数の式） y=ax+b 放物線の式 y=ax2 双曲線 y= x a グラフから式や座標を求める問題は頻出です。 グラフの特長と式の形を整理しておきましょう。 比例y=axのグラフは原点を通る直線ですので、１次関数でb=0のときと覚えておくと便利です。 4. 展開・因数分解の公式 単問の計算問題だけでなく、文章題で式をつくった後の計算で利用することもあります。 ２次方程式を解く際にも役立ちます。 5. 合同条件・相似条件 図形の証明問題で必須です。減点対象にもなるので、正確に書けるように覚えましょう。 辺の長さを求めるときに、図形が合同、相似であることを利用する場合もあります。 6. 円周角の定理 円に関する図形問題で、角度を求めるときによく使われます。 図形の中に円や弧を見つけたら、円周角の定理を意識して角度を調べてみましょう。 7. 多角形の内角の和・外角の和 基本的な図形問題や証明問題で使われます。 どんな多角形でも外角の和は360°ですので、外角から考えると計算しやすくなる場合もあります。 入試での使われ方と注意点 高校入試では、公式をただ覚えているだけでは点数につながりません。 公式が「どんなパターンで出題されるか」を知り、「使いこなす力」を身につけることが何よりも重要です。 例えば、三平方の定理は、関数や空間図形の中に隠れていることもあります。 公式を使えるようになるために、様々な問題を解くことが何よりも大切です。 また、一つの問題で複数の公式を組み合わせるパターンもよく出題されます。 公式を単独で覚えるだけでなく、それぞれの公式がどう連携し合っているのか、全体像を意識して学習に取り組みましょう。 「なぜそうなるか」から数学公式を理解する 公式を丸暗記するだけでは、少し問題がひねられると対応できなくなってしまいます。 公式が「なぜそうなるのか」、その成り立ちを理解することで、忘れにくく、応用も効く「使える知識」になります。 • ２次方程式の解の公式 なぜあの複雑な形になるのか？ これは平方完成という考え方から導き出されます。 式の変形を順を追って理解することで、公式がより深く頭に残ります。 • 三平方の定理 なぜ a2+b2=c2 なのか？ これは、直角三角形の各辺を一辺とする正方形の面積の関係を表しています。 図を使って考えることで、視覚的に理解を深められます。 • 円周角の定理 なぜ「中心角の半分になる」のか？ これは補助線をひいて、二等辺三角形の性質を使うと、簡単に証明できます。 このように、「なぜ？」という疑問を持つことは、数学の面白さを発見する第一歩です。 公式を使って問題をたくさん解くとともに、その公式がなぜ成り立つのか調べてみると理解が深まります。 覚え方・使いこなし練習 公式を覚えるには、ただ眺めているだけでは不十分です。 効果的な覚え方と、実際に使いこなすための練習法を知ることが、記憶定着と応用力アップのカギとなります。 語呂合わせ・図解を活用しよう 文字ばかりの公式を覚えるのが苦手なら、語呂合わせや図解を積極的に活用しましょう。 例えば、球の表面積や体積の公式などは語呂合わせがあります。 ・球の表面積は、「心配（4π）あるある（r2）」 ・球の体積は、「身の上に心配（ 4π 3 ）あるから参上（r3）」 公式を覚えるときに、自分だけの語呂合わせをつくってみましょう。 友達と共有しても面白いかもしれません。 円周角の定理などは、図で視覚的に理解する方が記憶に残りやすいです。 図解が必要な公式は、自分で簡単な絵をかいたり、教科書や参考書の図をじっくり見たりして、「なぜこうなっているんだろう？」と考えてみましょう。 視覚を利用して覚えることで、いざという時に「あの図だ！」と思い出しやすくなります。 公式を使う練習のすすめ 公式は、問題演習とセットで覚えることが記憶定着のコツです。 覚えた公式を、実際に問題を解きながら使ってみることで、その使い方や、どんな時に使うべきかが自然と身につきます。 間違えた問題は、なぜ間違えたのか、どの公式の使い方が間違っていたのかをしっかり確認し、もう一度解き直しましょう。 この繰り返しが、公式を「使える力」に変える最も効果的な方法です。 おすすめの学習教材 公式の理解と定着を深めるためには、適切な教材選びも重要です。 ここで、皆さんの学習を強力にサポートしてくれる教材をご紹介します。 ◆ 中学教科書ワーク 学校の教科書の内容に沿ってつくられているため、日々の授業の予習・復習に最適です。 イラストや図解が豊富で、数学の公式も詳しく解説されています。 高校入試に有効な問題も多くふくまれており、基礎から応用まで着実に力をつけることができます。 ▶シリーズページはこちら ▶ご購入はこちら ◆ わからないをわかるにかえる ニガテなところがどんどんわかる！超基礎からやさしく学べる、中学生のための問題集！ 数学の基本的な問題の解き方を丁寧に解説しています。 公式も覚えやすくなるよう配慮していますので、数学が苦手な方でも大丈夫。 小学生の先取り学習や、高校生・大人の学び直しにもおすすめです。 学年別・領域別と、高校入試シリーズがあります。 ▶シリーズページはこちら ▶ご購入はこちら ◆ 完全攻略 教科書だけではもの足りないキミに送る、定期テスト対策から高校入試の基礎固めに最適な問題集です。 ▶シリーズページはこちら ▶ご購入はこちら ◆ ハイクラス徹底問題集 最高峰の問題演習で、「試験に強い実力」をつけられる問題集です。レベルの高い問題にチャレンジしたい方に最適です。 ▶シリーズページはこちら ▶ご購入はこちら まとめ 公式を「使える力」に変えよう ここまで、中学数学の公式について、その種類から高校入試での重要性、そして効果的な学習法まで、幅広く紹介してきました。 大切なのは、公式を「知る」→「理解する」→「使えるようになる」という段階をしっかり踏むことです。 丸暗記ではなく、「なぜそうなるのか」を考え、実際に問題を解きながら使いこなす練習を続けましょう。 それが、数学の力を大きく伸ばすカギとなります。 紹介した文理の教材をうまく活用し、公式を「使える力」に変えて、自信を持って高校入試に挑んでくださいね。 皆さんの学習がより充実したものになるよう、心から応援しています！
